Classificação de doenças usando dados de expressão gênica

Este post apresenta um relatório sobre os passos utilizados na resolução do projeto de predição de doenças utilizando Microarrays disponível no KDnuggets e foi realizado em parceria com a Clarissa Simoyama David.
Os organismos vivos são constituídos por células com objetivos bem específicos, como representar pele, sangue, músculos, neurônios, entre outros. Cada célula possui um núcleo celular que contém o material genético das células, composto por cromossomos que são formados a partir de genes que são sequências de DNA (Ácido Desoxirribonucleico).
Segundo COLOMBO e RAHAL (2010), uma das ferramentas que pode ser utilizada para analisar a expressão gênica de milhares de genes é o Microarray.
Este projeto tem como objetivo utilizar algumas amostras de expressão gênica (microarray) para elaborar um modelo capaz de classificar cinco tipos de doenças EPD, JPA, MED, MGL e RHB. Os dados das amostras de exemplos estão disponíveis no site do KDnuggets.
Os exemplos disponibilizadas são compostos por 69 amostras cada uma contendo 7.070 genes e estão disponíveis no arquivo pp5i_train.gr.csv. Este arquivo está representado por um arquivo no formato .csv em que as colunas representam os 69 microarrays e as linhas representam os 7.070 genes, como apresentado na Tabela 1.
Tabela 1: Exemplos de treinamento disponíveis no arquivo pp5i_train.gr.csv.
| SNO | 1 | 2 | 3 | … | 69 |
|---|---|---|---|---|---|
| A28102_at | 30 | 46 | 31 | … | 38 |
| AB000114_at | 22 | 31 | 19 | … | 17 |
| … | … | … | … | … | … |
| Z78285_f_at | 0 | -1 | -2 | … | 3 |
Estas 69 amostras de exemplos já foram devidamente classificadas e suas classes foram disponibilizadas no arquivo pp5i_train_class.txt, como apresentado na Tabela 2.
Tabela 2: Classes dos exemplos de treinamento disponíveis no arquivo pp5i_train_class.txt.
| Class |
|---|
| MED |
| MED |
| … |
| JPA |
A partir do arquivo pp5i_train.gr.csv e pp5i_train_class.txt deve ser elaborado um modelo de classificação que aprenda a classificar novas amostras de exemplos. Para avaliar o desempenho do modelo foi disponibilizado um arquivo de testes chamado pp5i_test.gr.csv, este arquivo possui 23 amostras de exemplos também contendo 7.070 genes, que não foi previamente rotulado, como mostrado na Tabela 3.
Tabela 3: Exemplos de testes disponíveis no arquivo pp5i_test.gr.csv.
| SNO | 101 | 102 | 103 | … | 123 |
|---|---|---|---|---|---|
| A28102_at | 58 | 52 | 13 | … | 119 |
| AB000114_at | 36 | 34 | 32 | … | 53 |
| … | … | … | … | … | … |
| Z78285_f_at | 0 | -1 | 2 | … | -8 |
Por tanto, este trabalho tem como objetivo analisar estes dados de testes e classificar a doença a que cada amostra de exemplo se refere.
A elaboração do modelo de classificação foi realizado da seguinte maneira: inicialmente foi realizado uma limpeza dos dados recebidos; depois foi selecionado os melhores genes de cada classe de doença; foram avaliados alguns classificadores; e o melhor classificador foi utilizado para rotular os dados de testes. Cada um destes processos foi detalhado nas seções seguintes.
Limpeza dos dados
Antes de iniciar o treinamento do modelo classificador foi necessário realizar a limpeza dos dados. Segundo os biólogos, nestes experimento, os valores de expressão gênica menores que 20 e maiores que 16.000 não são confiáveis.
Para tratar tal situação, o primeiro passo de pré-processamento realizado foi aplicar a normalização nos dados conforme apresentado no Algoritmo 1.
Algoritmo 1: Algoritmo de normalização que mantém os valores entre o intervalo [20, 16.000].
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
Entrada: Este algoritmo recebe como entrada o valor de *nomeArquivo*,
que representa nome do arquivo que contêm os valores dos genes que
serão normalizados.
Saida: Como resultado será gerado um novo arquivo com o nome no padrão
*norm_ + nomeArquivo* com os valores de expressão gênica normalizados.
Inicio:
//A função lerArquivo devolve todas as linhas contidas no arquivo.
entrada = lerArquivo(nomeArquivo);
//A função criarArquivo cria um novo arquivo para saída dos dados.
arquivoSaida = criarArquivo('norm_' + nomeArquivo);
//Pula a primeira linha de cabeçalho.
Para i = 1; i < entrada.length; i++:
//Separa os valores da linha.
genes = entrada[i].split(',');
//Pula a primeira coluna que representa a descrição do gene.
Para j = 1; j < genes.length; j++:
valor = genes[j];
Se valor < 20:
valor = 20;
Senão Se valor > 16000:
valor = 16000;
arquivoSaida.escreve(valor);
//Subtrai 2 do tamanho por causa da coluna de descrição do gene.
Se j < genes.length - 2:
arquivoSaida.escreve(',');
//Subtrai 2 do tamanho por causa da linha de cabeçalho.
Se i < entrada.length - 2:
arquivoSaida.novaLinha();
Fim
O Algoritmo 1 gera dois novos arquivos, chamados norm_pp5i_train.gr.csv e norm_pp5i_test.gr.csv, que não contém cabeçalho e descrição dos genes, e tem os valores de expressão gênica restritos no intervalo [20, 16.000].
Seleção dos melhores genes por classe
O segundo passo do pré-processamento realizado foi a seleção dos melhores genes separados por classes. Para realizar este filtro, primeiro foi verificado a variação dos genes e removido dos dados de treinamento os genes com variação menor que 2, pois segundo os biólogos este passo é importante para avaliar a variabilidade genética.
Para calcular a variação genética foi identificado o gene de maior valor e de menor valor entre as amostras de microarray e aplicado a Equação 1.
Equação 1: Equação para encontrar a variação genética.
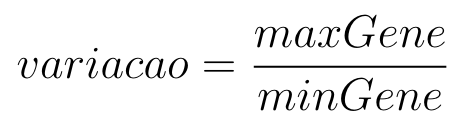
na qual o maxGene é o maior valor e minGene é o menor valor de um determinado gene entre todas as amostras de exemplos.
O Algoritmo 2 apresenta um pseudo-algoritmo aplicado para filtrar os genes com variação genética menor que 2.
Algoritmo 2: Algoritmo que filtra os genes com variação genética menor que 2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
Entrada: Este algoritmo recebe como entrada o valor de *nomeArquivo*, que
representa nome do arquivo que contêm os valores dos genes já normalizados
e que serão filtrados.
Saida: Como resultado será gerado um novo arquivo com o nome no padrão
*var_ + nomeArquivo* com os genes filtrados de acordo com a variação genética.
Inicio:
//A função lerArquivo devolve todas as linhas contidas no arquivo.
entrada = lerArquivo(nomeArquivo);
//A função criarArquivo cria um novo arquivo para saída dos dados.
arquivoSaida = criarArquivo(nomeArquivo.replace('norm', 'var_'));
Para i = 0; i < entrada.length; i++:
//Separa os valores da linha.
genes = entrada[i].split(',');
//Calcula a variação do gene.
variacao = max(genes) / min(genes);
Se variacao >= 2:
Para j = 0; j < genes.length; j++:
arquivoSaida.escreve(genes[j]);
Se j < genes.length - 1:
arquivoSaida.escreve(',');
Se i < entrada.length - 1:
arquivoSaida.novaLinha();
Fim
Como os 7.070 genes estão dispostos como linhas do arquivo norm_pp5i_train.gr.csv, no Algoritmo 2 todas as linhas são lidas e para cada linha é calculado os valores de maxGenes e minGenes por meio das funções max() e min(), respectivamente, calculado o valor da variacao, os genes cuja variação são maiores ou igual a 2 são gravados em outro arquivo chamado var_pp5i_train.gr.csv.
O arquivo var_pp5i_train.gr.csv, contendo apenas os genes cuja variação é maior ou igual a 2, ficou com 6.411 genes nas 69 amostras de exemplo.
A segunda parte da seleção dos melhores genes consiste em separar para cada classe um subconjunto com os melhores 2, 4, 6, 8, 10, 12, 15, 20, 25 e 30 genes.
Para identificar os melhores genes foi calculado o valor do T-Value dos genes separados por classe. Para calcular o T-Value foi utilizado a Equação 2.
Equação 2: Equação para encontrar a variação genética.
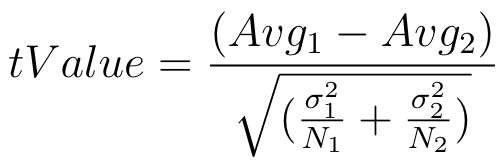
em que para cada classe C, o valor N_1 representa a quantidade de genes, Avg_1 representa a média dos valores dos genes e sigma_1 representa o desvio médio padrão desta classe, enquanto que o valor de N_2 representa a quantidade de genes, Avg_2 representa a média dos valores e sigma_2 representa o desvio médio padrão dos genes das demais classes.
O Algoritmo 3 apresenta um pseudo-algoritmo que utiliza os dados dos genes com variação maior ou igual a 2 e as classes das amostras de exemplos para calcular os T-Values e gera um novo arquivo chamado t_value_pp5i_train.gr.csv contendo todos os valores dos genes mais os valores dos T-Values.
Algoritmo 3: Algoritmo que calcula o valor dos T-Values por classe.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
Entrada: Este algoritmo recebe como entrada o valor de *nomeArquivoDados*,
que representa o nome do arquivo que contêm os valores dos genes com variação
maior ou igual a 2, e também o valor de *nomeArquivoClasses*, que representa
o nome do arquivo que contêm as classes dos exemplos.
Saida: Como resultado será gerado um novo arquivo com o nome no padrão
*t_value_ + nomeArquivoDados* contendo os valores dos genes e os *T-Values*
calculados para cada combinação de classes.
Inicio:
nomeClasses = {'MGL', 'EPD', 'JPA', 'MED', 'RHB'};
entrada = lerArquivo(nomeArquivoDados);
classes = lerArquivo(nomeArquivoClasses);
arquivoSaida = criarArquivo(nomeArquivoDados.replace('var_', 't_value'));
Para i = 0; i < entrada.length; i++:
genes = entrada[i].split(',');
lista = classesComGenes(entrada);
avgStdevs = calcularAvgStdevs(lista);
tValues = calcularTValues(avgStdevs);
Para j = 0; j < genes.length; j++:
arquivoSaida.escreve(genes[j]);
Se j < genes.length - 1:
arquivoSaida.escreve(',');
Para cada tValue em tValues:
arquivoSaida.escreve(',' + tValue);
Se i < entrada.length - 1:
arquivoSaida.novaLinha();
Fim
Para realizar o calculo dos T-Values foram criados mais três algoritmos específicos, sendo eles: o Algoritmo 4 que monta uma lista contendo um mapa para cada um dos 6.411 genes agrupando os genes de acordo com a classe do microarray; depois o Algoritmo 5 que calcula os valores das médias e desvios padrões para cada gene; e por fim o Algoritmo 6 calcula os valores dos T-Values para cada classe.
Como tem cinco classes diferentes foram calculados cinco valores T-Values, pois para cada classe o valor do T-Value é calculado com relação as outras demais quatro classes existentes.
Algoritmo 4: Algoritmo que elabora um mapa para cada gene, agrupando-os de acordo com a classe do microarray.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Entrada: Este algoritmo recebe um vetor de *genes* como entrada.
Saida:Como resultado gera uma lista contendo um mapa para cada gene,
agrupando este gene de cada *microarray* de acordo com a classe.
Inicio:
lista = ();
Para i = 0; i < entrada.length; i++:
genes = entrada[i].split(',');
mapa = {};
Para j = 0; j < genes.length; j++:
mapa[classe[i]] += genes[j];
lista += mapa;
return lista;
Fim
Algoritmo 5: Algoritmo que monta uma lista contendo para cada gene o valor da média, desvio médio padrão e a quantidade de microarrays.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Entrada: Este algoritmo recebe como entrada uma *lista* contendo um mapa
para cada gene que agrupa os genes dos *microarrays* de acordo com a classe.
Saida: Como resultado será gerado uma lista contendo para cada gene o valor
da média, desvio médio padrão e a quantidade de *microarrays*.
Inicio:
nomeClasses = {'MGL', 'EPD', 'JPA', 'MED', 'RHB'};
avgStdevs = ();
Para cada mapa em lista:
listaPorGene = ();
Para cada classe em nomeClasses:
n = mapa[classe].length
soma = sum(mapa[classe]);
avg = soma / n;
quadrado = sum(gene^2 em mapa[classe]);
stdev = sqrt(((n * quadrado) - (soma * soma)) / (n * (n - 1)));
listaPorGene += [avg, stdev, n]
avgStdevs += listaPorGene;
return avgStdevs;
Fim
Algoritmo 6: Algoritmo que calcula o valor dos T-Values para cada gene separados por classes.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
Entrada: Este algoritmo recebe como entrada uma lista contendo para cada
gene o valor da média, desvio médio padrão e a quantidade de *microarrays*.
Saida: Como resultado será gerado uma lista contendo para cada gene cinco
valores de *T-Value* sendo um para cada classe.
Inicio:
tValues = ();
Para cada avgStdev em avgStdevs:
tValuesPorGene = ();
Para i = 0; i < avgStdev.length; i++:
avg1 = avgStdev[i][0];
stdev1 = avgStdev[i][1];
n1 = avgStdev[i][2];
avg2, stdev2, n2 = 0;
Para j = 0; j < avgStdev.length; j++:
Se i != j:
avg2 = avgStdev[j][0];
stdev2 = avgStdev[j][1];
n2 = avgStdev[j][2];
avg2 = avg2 / 4;
stdev2 = stdev2 / 4;
tValuesPorGene += (avg1 - avg2) / (sqrt((stdev1 * stdev1 / n1)
+ (stdev2 * stdev2 / n2)));
tValues += tValuesPorGene;
return tValues;
Fim
Com base no arquivo t_value_pp5i_train.gr.csv serão selecionados os genes por classe de acordo com o valor absoluto do T-Value.
O Algoritmo 7 gera um arquivo pp5i_train.topN.gr.csv para cada N = 2, 4, 6, 8, 10, 12, 15, 20, 25 e 30, este arquivo contém a combinação dos melhores genes de cada classe removendo os exemplos duplicados.
Algoritmo 7: Algoritmo que gera os arquivos separados com os melhores 2, 4, 6, 8, 10, 12, 15, 20, 25 e 30 genes.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
Entrada: Este algoritmo recebe como entrada o valor de *nomeArquivo*, que
representa nome do arquivo que contêm os valores dos genes e dos *T-Values*.
Saida: Como resultado será gerado arquivos separados com os melhores 2, 4,
6, 8, 10, 12, 15, 20, 25 e 30 genes por classe sem os duplicados.
Inicio:
entrada = lerArquivo(nomeArquivo);
Para cada top em {2, 4, 6, 8, 10, 12, 15, 20, 25, 30}:
// O valor do T-Value da primeira classe começa na coluna 69.
Para posTValue = 69; posTValue < dados.length; posTValue++:
//Um simples BubbleSort para ordenar os exemplos pelo T-Value,
//lembrando que é a ordem absoluta dos valores.
Para i = 0; i < entrada.length - 1; i++:
Para j = i + 1; j < entrada.length; j++:
Se abs(entrada[i][posTvalue]) < abs(entrada[j][posTvalue]):
temp = entrada[i];
entrada[i] = entrada[j];
entrada[j] = temp;
arquivoSaida = criarArquivo('pp5i_train.top' + top + '.gr.csv');
melhores = ();
Para i = 0; i < top; i++:
//Não adiciona genes duplicados.
Se entrada[i] não está em melhores:
melhores += entrada[i];
//Não salva os T-Values no arquivo de saída.
Para j = 0; j < entrada[i].length - 5; j++:
arquivoSaida.escreve(entrada[i][j]);
Se j < entrada[i].length - 6:
arquivoSaida.escreve(',');
Se i < top.length - 1:
arquivoSaida.novaLinha();
Fim
No fim do pré-processamento, o Algoritmo 8 realiza a transposta dos dados, de modo que cada linha represente um microarray e cada coluna represente os genes, no final de cada linha inclui a classe e gera um arquivo pp5i_train.topN.gr.arff no formato ARFF, como apresentado a seguir:
1
2
3
4
5
6
7
8
9
10
11
@RELATION treinamento
@ATTRIBUTE atributo1 NUMERIC
@ATTRIBUTE atributo2 NUMERIC
@ATTRIBUTE atributoN NUMERIC
@DATA
20.0,74.0,49.0,20.0,27.0,89.0,105.0,188.0,20.0,20.0,MED
20.0,68.0,31.0,20.0,45.0,88.0,60.0,131.0,20.0,20.0,MED
...
119.0,76.0,54.0,29.0,143.0,200.0,209.0,826.0,92.0,159.0,JPA
Algoritmo 8: Algoritmo que converte os arquivos CSVs com os melhores 2, 4, 6, 8, 10, 12, 15, 20, 25 e 30 genes para o formato ARFF.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
Entrada: Este algoritmo recebe como entrada o valor de *nomeArquivoClasses*,
que representa nome do arquivo que contêm as classes das amostras de exemplos.
Saida: Como resultado será gerado arquivos ARFFs os melhores 2, 4, 6, 8, 10,
12, 15, 20, 25 e 30 genes.
Inicio:
Para cada top em {2, 4, 6, 8, 10, 12, 15, 20, 25, 30}:
entrada = lerArquivo('pp5i_train.top' + top + '.gr.csv');
classes = lerArquivo(nomeArquivoClasses);
arquivoSaida = criarArquivo('pp5i_train.top' + top + '.gr.arff');
entrada = entrada^t;
arquivoSaida.escreve('@RELATION treinamento');
arquivoSaida.pulaLinha();
Para i = 1; i <= top; i++:
arquivoSaida.escreve('@ATTRIBUTE atributo' + i + ' NUMERIC')
arquivoSaida.pulaLinha();
}
arquivoSaida.escreve('@ATTRIBUTE Class {MED,MGL,RHB,EPD,JPA}');
arquivoSaida.pulaLinha();
arquivoSaida.escreve('@DATA');
arquivoSaida.pulaLinha();
Para i = 0; i < entrada.length; i++:
arquivoSaida.escreve(entrada[i] + ',' + classes[i]);
Se i < entrada.length - 1:
arquivoSaida.pulaLinha();
Fim
Seleção do melhor classificador e melhor combinação de atributos
Seguindo o guia do projeto, foi realizada classificação de cada topN gerado utilizando os algoritmos do WEKA, com validação cruzada de k = 10 folds. Foram utilizados cinco classificadores: NaiveBayes, J48, IBk variando o valor de k (k = 2, 3, 4), IB1 e K* (KStar). E por fim é apresentado os resultados dos classificadores e a melhor combinação de atributos encontrada.
NaiveBayes
O Naive Bayes (ZHANG, 2004) é um modelo de probabilidade condicional. Dado uma instância de dados x = (x_1, x_2, …, x_n), assume-se que cada dimensão de x é totalmente independente da outra. O Naive Bayes calcula a probabilidade de um exemplo de dados x pertencer a uma classe C (P ( C | x)). Usando o teorema de Bayes, essa probabilidade pode ser reescrita como a Equação 3.
Equação 3: Equação que utiliza o teorema de Bayes para calcular a probabilidade que um exemplo possui em relação a uma classe.
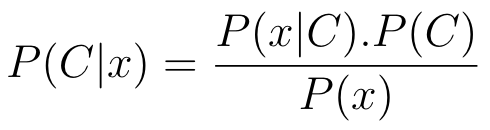
O Naive Bayes considera que cada atributo x_i da entrada de dados é independente, dessa forma, podemos reescrever a fórmula anterior como a Equação 4.
Equação 4: Reescrevendo a Equação anterior para cada atributo x_i.
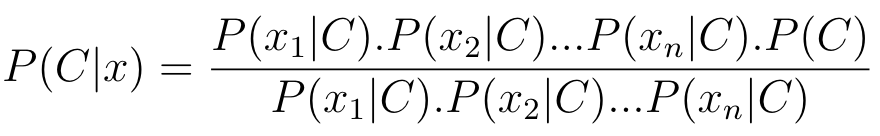
Para cada classe possível do problema, há uma probabilidade P(C | x) diferente. Para definir a qual classe o exemplo pertence, escolhe-se a classe com maior probabilidade.
J48
O algoritmo J48 pertencente ao WEKA é a implementação do classificador C4.5 (QUIN-LAN, 1993), que geram árvores de decisão dado um conjunto de dados rotulados. A árvore de decisão é uma estrutura de dados de fluxo que simulam uma árvore, sendo os nós internos denotando testes de atributos, os ramos representando os resultados dos testes e os nós folhas consistindo dos rótulos ou distribuição das classes. São testados os valores dos atributos de cada instância na árvore de decisão a partir da raiz até uma das folhas. A geração da árvore consiste em duas fases:
- Construção da árvore: todas as instâncias de treinamento estão na raiz da árvore. As instâncias são particionadas recursivamente, com base em seus valores de atributos;
- Poda da árvore: são identificados e removidos ramos que possam representar outliers e ruídos para a árvore.
IBk
O algoritmo IBk pertencente ao WEKA é a implementação do classificador KNN (classificador vizinho mais próximo) (OVER e HART, 1967). A classificação de cada elemento no espaço é feita de acordo com a distância entre os k objetos mais próximos do elementos. Isso é possível pois é realizado um treinamento com uma base teste e com uma base de treinamento. Normalmente a métrica utilizada para calcular a distância entre os objetos é a distância euclidiana, vista na Equação 5, sendo n o número de dimensões, i a coordenada atual calculada, x_{i} e y_{i} os valores das coordenadas dos dois pontos.
Equação 5: Equação da distância euclidiana.
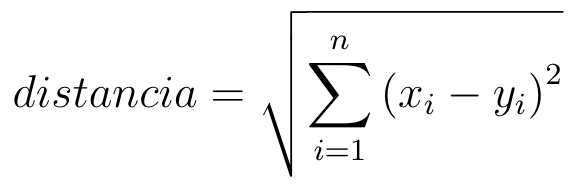
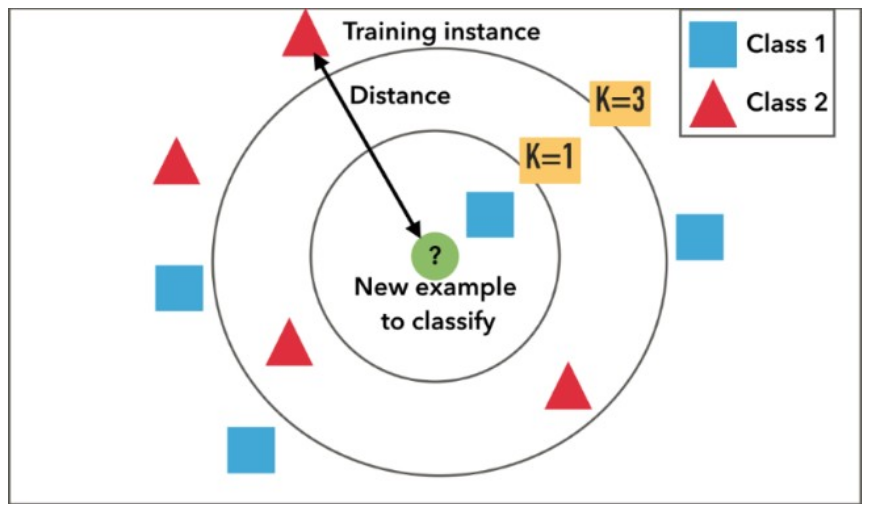
Uma decisão importante é a escolha do número k de vizinhos, como visto na Figura 1, pois se o k for um número pequeno pode não considerar elementos próximos e importantes na classificação. Por outro lado, se k for um número grande, pode haver problemas em definir qual grupo o elemento pertence, pois a comparação é feita com diversos vizinhos diferentes, além de possuir um custo computacional maior.
Figura 1: Exemplo do algoritmo KNN visto graficamente.
IB1
O algoritmo IB1 é um caso específico do algoritmo IBk, no qual o valor de k = 1, mas a classificação sendo feita da mesma forma do IBk.
K*
O classificador K* é baseado em instâncias. As classes das instâncias que pertencem a parte de teste são classificadas baseando-se em classes das instâncias que pertencem à parte de treinamento que são similares à elas, com alguma função de similaridade. O principal diferencial do classificador K* é que, diferentemente de outros classificadores baseados em instâncias, ele utiliza uma função de distância baseada em entropia (CLEARY e TRIGG, 1995), isto é, a distância entre instâncias é definida pela complexidade de transformar uma instância em outra. Tanto atributos reais quanto atributos simbólicos podem ser utilizados juntos no algoritmo. O cálculo dessa complexidade é feito em duas etapas:
- Define-se um conjunto finito de transformações que mapeia instância por instância;
- Para a transformação de uma instância à outra é feita uma sequência finita de transformações, começando em uma e terminando em outra.
Resultados dos classificadores
Para cada classificador escolhido, foi medida a taxa de acurácia no conjunto de treinamento das instâncias previamente geradas com topN = 2, 4, 6, 8, 10, 12, 15, 20, 25, 30 genes. Os resultados podem ser vistos na Tabela 4 e graficamente na Figura 2.
Tabela 4: Resultado das acurácia dos classificadores.
| topN | NaiveBayes | J48 | IB1 | IBk (k = 2) | IBk (k = 3) | IBk (k = 4)} | K* |
|---|---|---|---|---|---|---|---|
| 2 | 94,2029 | 89,8551 | 97,1014 | 97,1014 | 95,6522 | 95,6522 | 97,1014 |
| 4 | 97,1014 | 88,4058 | 97,1014 | 98,5507 | 98,5507 | 97,1014 | 94,2029 |
| 6 | 95,6522 | 86,9565 | 98,5507 | 94,2029 | 97,1014 | 97,1014 | 98,5507 |
| 8 | 97,1014 | 86,9565 | 98,5507 | 95,6522 | 97,1014 | 97,1014 | 97,1014 |
| 10 | 94,2029 | 91,3043 | 98,5507 | 95,6522 | 98,5507 | 98,5507 | 95,6522 |
| 12 | 92,7536 | 91,3043 | 100 | 95,6522 | 100 | 98,5507 | 97,1014 |
| 15 | 94,2029 | 97,1014 | 100 | 98,5507 | 100 | 98,5507 | 97,1014 |
| 20 | 97,1014 | 97,1014 | 98,5507 | 100 | 98,5507 | 98,5507 | 100 |
| 25 | 98,5507 | 97,1014 | 100 | 98,5507 | 98,5507 | 97,1014 | 98,5507 |
| 30 | 98,5507 | 97,1014 | 98,5507 | 95,6522 | 97,1014 | 97,1014 | 98,5507 |
Figura 2: Resultado dos classificadores em questão de acurácia.
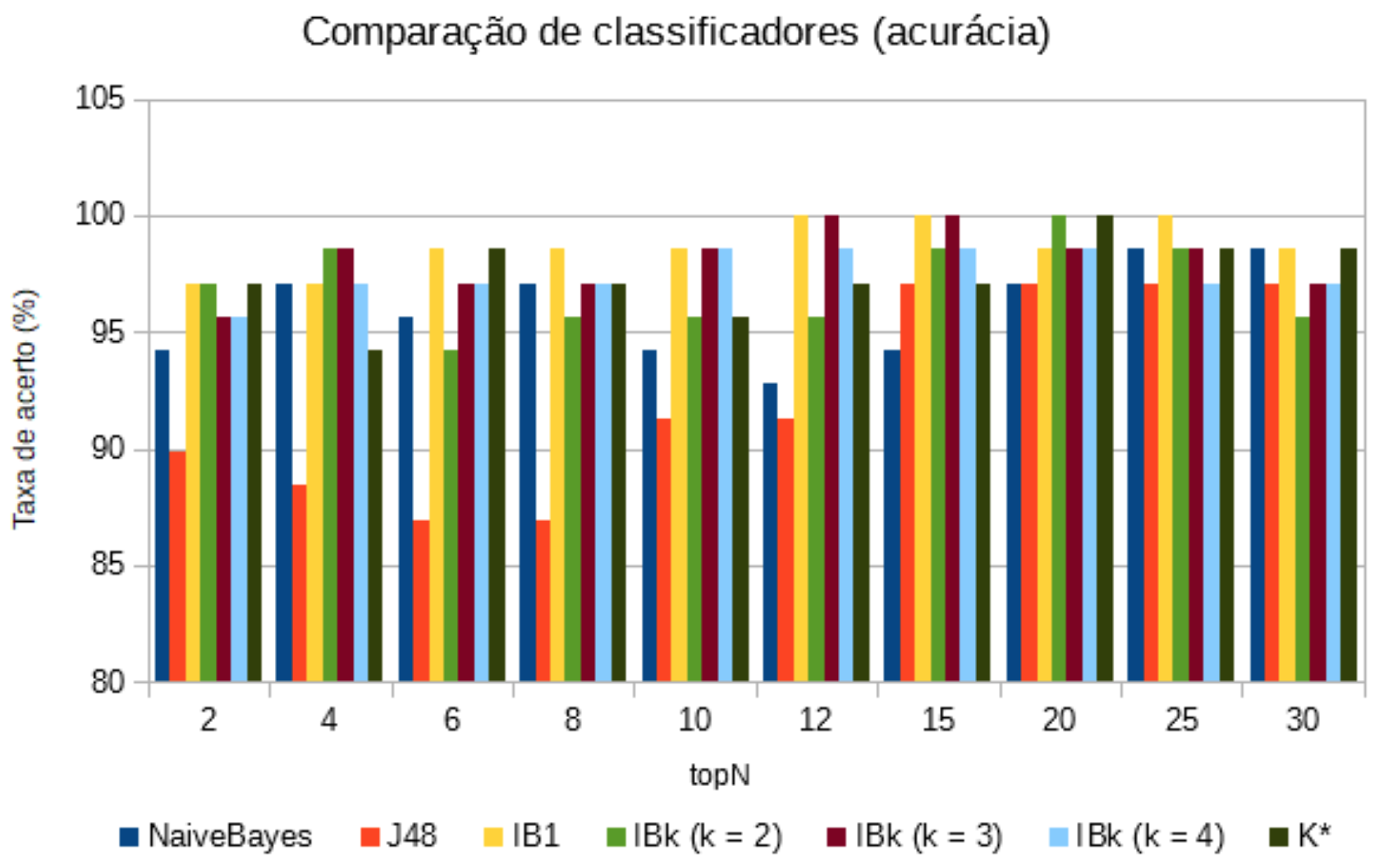
Também foi coletado os resultados dos erros médios de cada classificador em cada topN. Os resultados podem ser vistos na Tabela 5 e graficamente na Figura 3.
Tabela 5: Resultado dos erros médio dos classificadores.
| topN | NaiveBayes | J48 | IB1 | IBk (k = 2) | IBk (k = 3) | IBk (k = 4) | K* |
|---|---|---|---|---|---|---|---|
| 2 | 0,0266 | 0,0447 | 0,0346 | 0,0263 | 0,0328 | 0,0361 | 0,0198 |
| 4 | 0,0116 | 0,0464 | 0,0346 | 0,0207 | 0,0215 | 0,0248 | 0,0212 |
| 6 | 0,0174 | 0,0522 | 0,0292 | 0,0263 | 0,0253 | 0,0205 | 0,0065 |
| 8 | 0,0117 | 0,0522 | 0,0292 | 0,0235 | 0,0197 | 0,0219 | 0,0116 |
| 10 | 0,0209 | 0,0348 | 0,0292 | 0,0235 | 0,0159 | 0,0163 | 0,0177 |
| 12 | 0,029 | 0,0348 | 0,0239 | 0,0207 | 0,014 | 0,0163 | 0,0116 |
| 15 | 0,0232 | 0,0116 | 0,0239 | 0,0152 | 0,0178 | 0,0205 | 0,0116 |
| 20 | 0,0116 | 0,0116 | 0,0292 | 0,018 | 0,0197 | 0,0248 | 0 |
| 25 | 0,0058 | 0,0116 | 0,0239 | 0,018 | 0,0215 | 0,0305 | 0,0056 |
| 30 | 0,0058 | 0,0116 | 0,0292 | 0,0235 | 0,0253 | 0,0276 | 0,0071 |
Figura 3: Resultado dos classificadores em questão do erro médio.
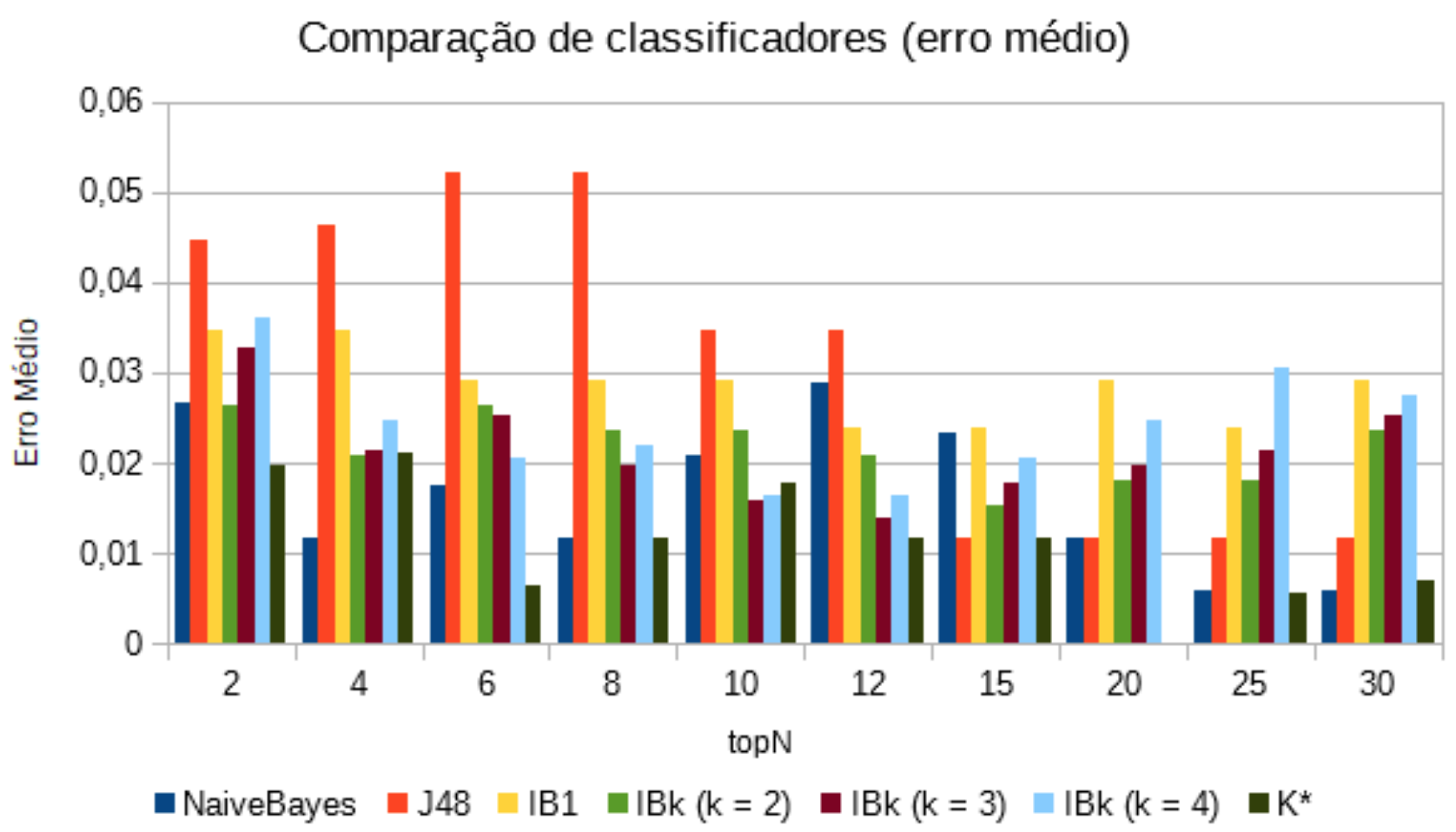
Para selecionar o modelo e a quantidade de atributos ideal a ser utilizado, foram observados o classificador com a maior taxa de acurácia juntamente com o menor valor de erro médio. Levando em conta estes quesitos, o modelo escolhido foi com topN = 20, com o classificador K*, que possui taxa de acurácia de 100% e erro médio de valor 0.
Os nomes dos genes que foram escolhidos do melhor conjunto de treinamento foram no total 84, que podem ser vistos na Tabela 6.
Tabela 6: Identificação dos melhores genes escolhidos do conjunto de treinamento.
| U00921_at | S80343_at | L39833_at | Z26248_s_at | U32331_at |
| U45955_at | M57464_s_at | U80184_rna1_at | U25956_at | X59372_at |
| Z83804_at | U48705_rna1_s_at | M84349_at | L10373_at | AF000424_s_at |
| M15661_at | L20971_at | U96769_rna1_at | U83463_at | U31383_at |
| M59488_at | M31520_rna1_s_at | U90911_at | HG620-HT620_at | X60188_at |
| X61587_at | M63623_at | U52828_s_at | U58046_s_at | X60787_s_at |
| U48250_at | M16447_at | L08895_at | U59877_s_at | D16181_at |
| U72263_s_at | U39817_at | L39064_rna1_at | U79294_at | U24266_at |
| S69272_s_at | U96136_at | X85373_at | Y00318_at | X52213_s_at |
| U51336_at | U47101_at | D16481_at | S95936_at | U30827_s_at |
| Z56281_at | U33429_at | D87470_at | U90916_at | U90552_s_at |
| X99133_at | U49957_s_at | X52011_at | U35340_at | D13631_s_at |
| X79353_at | J04543_at | X99142_at | X79234_at | X14789_at |
| M10051_s_at | U73379_at | X51405_at | U07802_at | U67156_at |
| D29956_at | U79242_at | HG3255-HT3432_at | M93426_at | M75099_at |
| M31303_rna1_at | X59812_at | U09477_at | D83646_at | M86528_at |
| D25304_at | L36818_at | D63506_at | U95740_rna2_at |
A partir destes genes escolhidos, foram extraídos estes mesmos genes do conjunto de teste. O conjunto de teste possui 23 instâncias, não-rotuladas, que utilizaremos para fazer as predições de suas instâncias. O conjunto de testes foi convertido para que os genes ficassem nas colunas e as instâncias ficassem nas linhas e, na última coluna, foi acrescentada um atributo de classe, sendo preenchido com o carácter ‘?’.
Predição dos dados de teste
Renomeando o melhor documento de treinamento, o topN = 20 com 84 genes e 69 instâncias, ele foi chamado de pp5i_train.bestN.csv, juntamente com o seu arquivo correspondente arff. O seu correspondente de conjunto de teste foi renomeado para pp5i_test.bestN.csv, com a mesma quantidade de genes e 23 instâncias. O conjunto de testes foi convertido para o formato de arff, com exatamente o mesmo cabeçalho utilizado na base de treinamento, com a diferença de que no atributo classes eram preenchidos de ‘?’.
Utilizando este arquivo escolhido de treinamento, juntamente com o seu respectivo conjunto de testes, e foi gerado as predições das classes com o classificador K*. O resultado das predições de cada instância do conjunto de testes obtido pode ser visto na Tabela 7. Cada instância possui sua respectiva classe predita.
Tabela 7: Predições das classes do conjunto de teste.
| InstanceNumber | predictedClass |
|---|---|
| 1 | MGL |
| 2 | EPD |
| 3 | MED |
| 4 | MED |
| 5 | EPD |
| 6 | MED |
| 7 | MED |
| 8 | MED |
| 9 | EPD |
| 10 | JPA |
| 11 | JPA |
| 12 | MED |
| 13 | MED |
| 14 | MED |
| 15 | MED |
| 16 | MED |
| 17 | MGL |
| 18 | MED |
| 19 | MED |
| 20 | RHB |
| 21 | RHB |
| 22 | MED |
| 23 | MED |
Por fim, foi gerado um arquivo ARFF das predições e elas foram coletadas em um arquivo csv chamado predictionClass.
Conclusão
O projeto prático proporcionou a aplicação de técnicas tanto vistas em aulas quanto técnicas utilizadas em atividades que não puderam ser estudadas em aula, como o algoritmo K*, abrangendo a maioria dos temas estudados durante o quadrimestre, desde o pré-processamento de dados, até a seleção de atributos, classificação e predição de classes em conjuntos de testes.
Também foi importante a utilização de ferramentas práticas para a tarefa de classificação, como a ferramenta WEKA, além das implementações de algoritmos para o auxílio do projeto. É importante notar um resultado interessante na classificação dos conjuntos de treinamento, mesmo que classificadores como o IBk com k = 2, com topN = 20, tenha dado 100% de acurácia, seu erro médio ainda era maior do que o resultado do K*, com acurácia também de 100% para o topN = 20, mas com erro de valor 0. Comparando com outros algoritmos, seus valores de erros são em geral menores, possuindo também bons resultados de acurácia, mostrando o potencial do classificador.
Referências
CLEARY, J. G.; TRIGG, L. E. K. An instance-based learner using an entropic distancemeasure. In: 12th International Conference on Machine Learning. [S.l.: s.n.], 1995. p. 108–114.
COLOMBO, J.; RAHAL, P. A. Tecnologia de microarray no estudo do câncer de cabeça e pescoço. Revista Brasileira de Biociências, p. 64–72, 2010.
COVER, T.; HART, P. Nearest neighbor pattern classification. IEEE transactions on information theory, IEEE, v. 13, n. 1, p. 21–27, 1967.
QUINLAN, R. C4.5: Programs for Machine Learning. San Mateo, CA: Morgan KaufmannPublishers, 1993.
ZHANG, H. The optimality of naive bayes. AA, v. 1, n. 2, p. 3, 2004.