Decision Tree: Aprendendo a classificar flores do tipo Iris

O dataset de flores do tipo Iris é um dos mais básicos utilizado para ensinar como funciona um modelo de classificação.
Como podemos classificar uma flor?
O dataset de Iris é clássico e muito utilizado para ensinar como funciona modelos de classificação. A partir das caracteristicas da flor Iris, o objetivo é classificar (definir a classe / rótulo) de qual é o tipo dessa flor, entre três tipos possíveis: Versicolor, Setosa e Virginica.
A Figura 1 apresenta os três tipos da flor Iris: Versicolor, Setosa e Virginica:
Figura 1: Tipos de flores Iris.

Fonte: https://www.datacamp.com/community/tutorials/machine-learning-in-r
Este dataset é composto por cinco características: SepalLength (Comprimento da Sépala), SepalWidth (Largura da Sépala), PetalLength (Comprimento da Pétala), PetalWidth (Largura da Pétala) e class (Classe).
A Figura 2 mostra visualmente as características da flor Iris:
Figura 2: Características da flor Iris.

No UCI Machine Learning Repository tem vários conjuntos de dados diferentes e um deles é o Iris Dataset composto por 150 amostras, esse dataset foi criado pelo biólogo e estatístico Ronald Fisher. A seguir são apresentados alguns exemplos (cada exemplo representa as características de uma flor Iris) do dataset:
| SepalLength | SepalWidth | PetalLength | PetalWidth | Class |
|---|---|---|---|---|
| 5.1 | 3.5 | 1.4 | 0.2 | Iris-setosa |
| 5.0 | 3.3 | 1.4 | 0.2 | Iris-setosa |
| 7.0 | 3.2 | 4.7 | 1.4 | Iris-versicolor |
| 5.7 | 2.8 | 4.1 | 1.3 | Iris-versicolor |
| 6.3 | 3.3 | 6.0 | 2.5 | Iris-virginica |
| 5.9 | 3.0 | 5.1 | 1.8 | Iris-virginica |
Decision Tree
A Árvore de Decisão (Decision Tree) é um modelo que cria uma estrutura de árvore com a representação das possíveis decisões que podem ser tomadas permitindo separar as classes de dados de acordo com suas características. A Figura 3 apresenta uma representação da árvore de decisão:
Figura 3: Representação da Decision Tree.
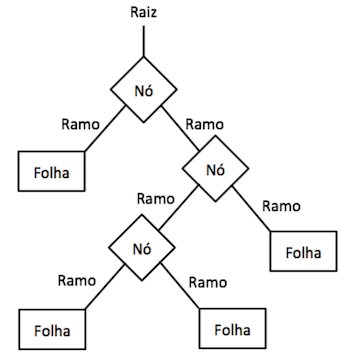
Cada Nó representa uma condição de decisão que é elaborada a partir das características. Ao percorrer as condições dos Nós chegamos até um nó final que é chamado de Folha que possui a classe que identifica essas características.
A ideia principal da Decision Tree é gerar uma árvore de condições lógicas, que consiga a partir das características e seus valores separar ou filtrar os exemplos que pertencem a cada ramificação, assim quando chegar ao Nó folha conseguimos identificar a qual classe pertence os exemplos.
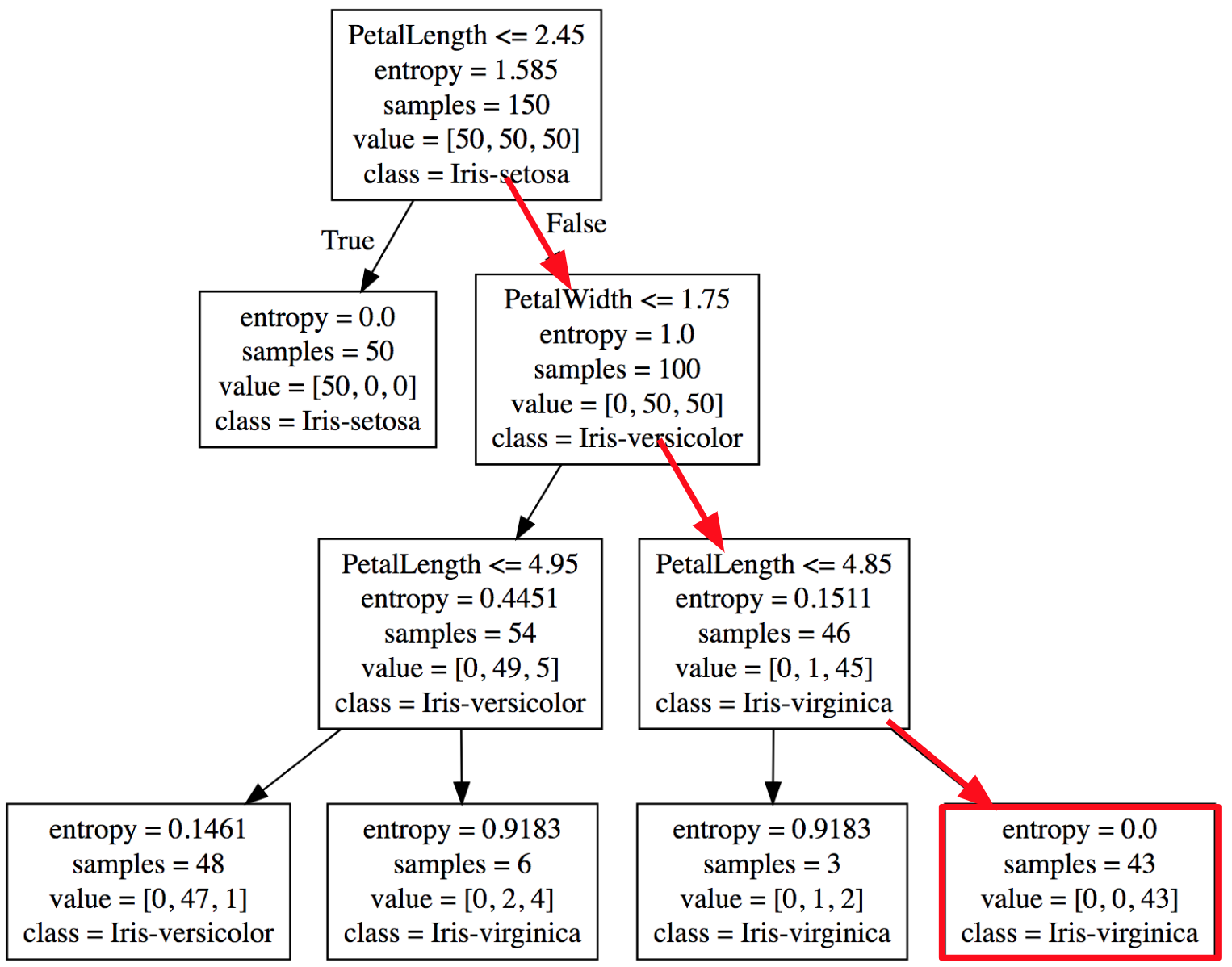
No exemplo das flores Íris, teremos três classes diferentes que serão identificadas nas folhas da árvore. A Figura 4 apresenta um exemplo de estrutura de Decision Tree que foi gerada a partir do dataset de Iris:
Figura 4: Decision Tree treinada com o dataset de flores Iris.
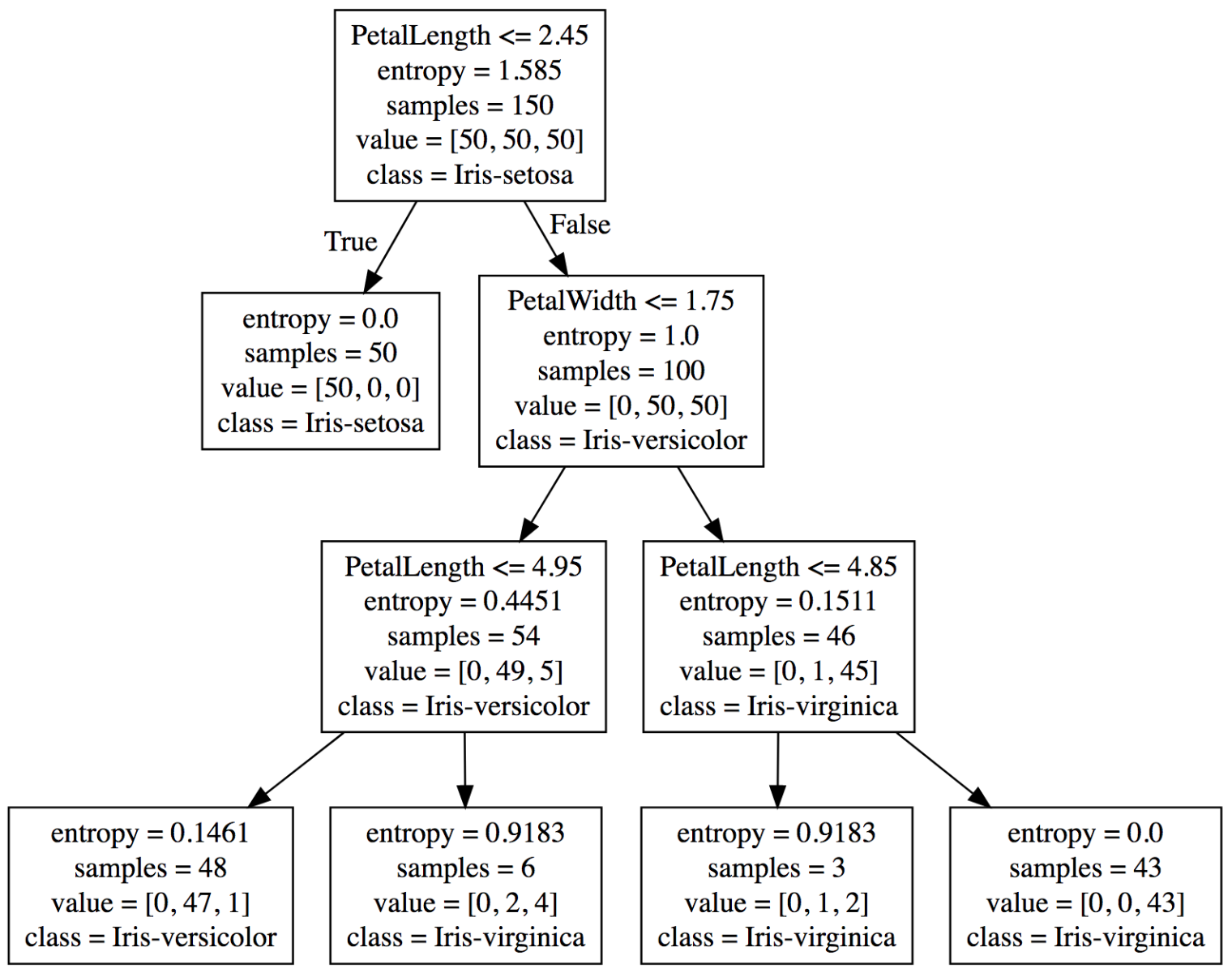
O primeiro Nó decide que se a característica PetalLenght for menor ou igual a 2.45, então deve seguir para o lado esquerdo da árvore, caso contrário segue para o lado direito da árvore.
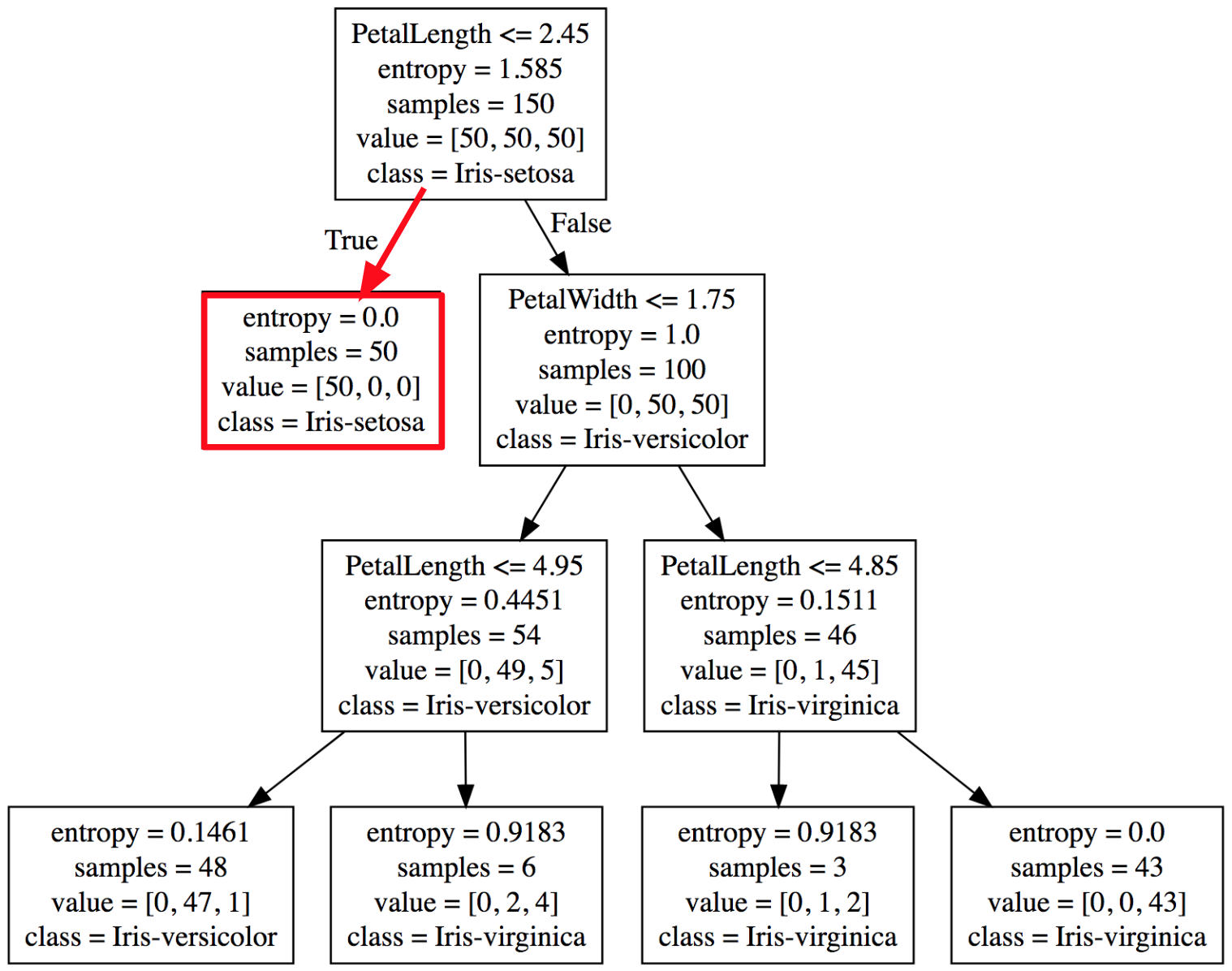
Então, se uma amostra (um exemplo que representa uma flor) com as características:
| SepalLength | SepalWidth | PetalLength | PetalWidth |
|---|---|---|---|
| 5.0 | 3.6 | 1.6 | 0.5 |
Podemos facilmente percorrer a árvore para identificar a classe com base nessas característica, como mostrado na Figura 5. Nesse exemplo podemos classificar essa flor como uma Iris-setosa.
Figura 5: Percorrendo o dataset para encontrar a classe Iris-setosa.
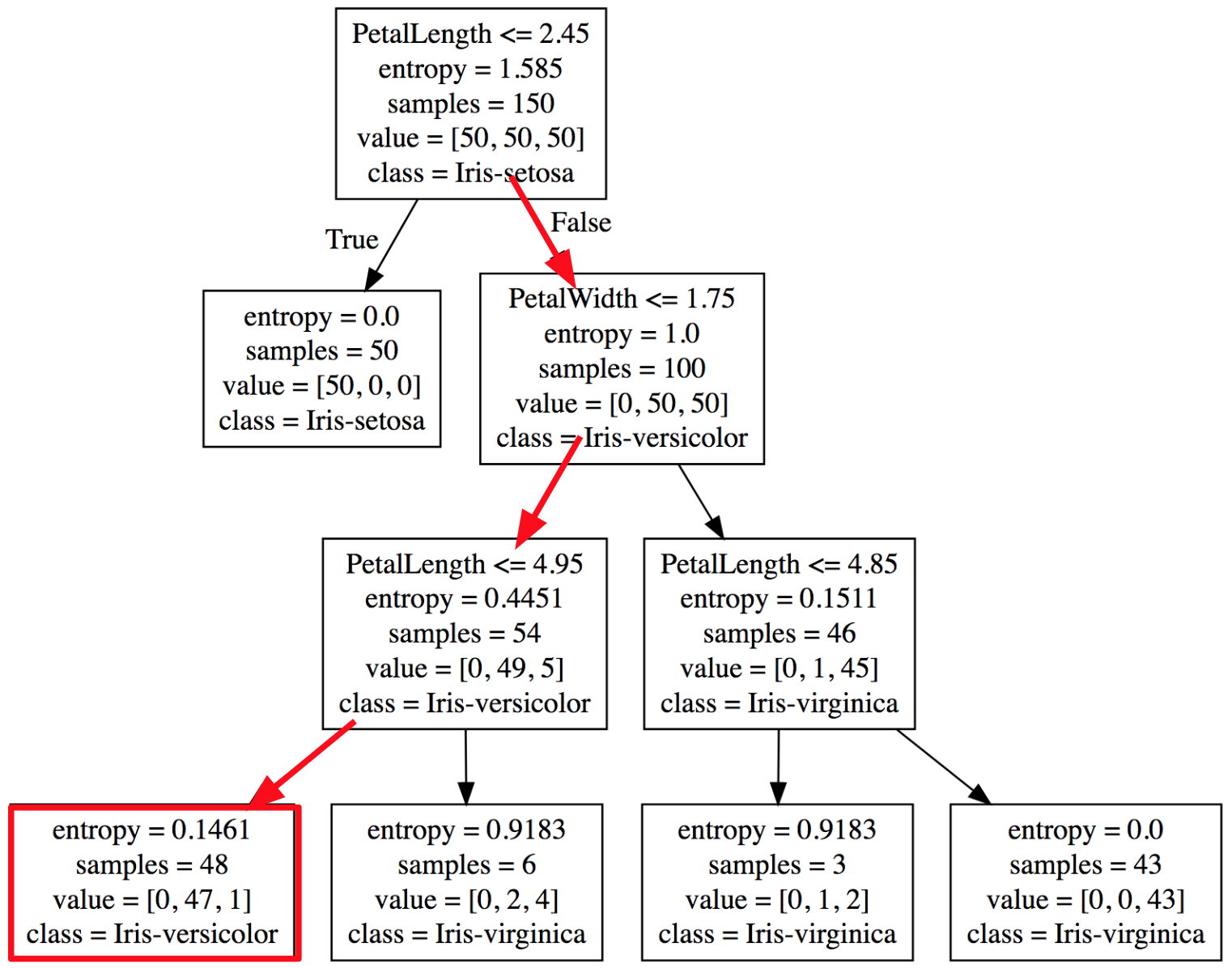
Utilizando uma amostra com as características:
| SepalLength | SepalWidth | PetalLength | PetalWidth |
|---|---|---|---|
| 5.8 | 2.7 | 4.2 | 1.2 |
Podemos percorrer cada Nó a partir das suas condições até chegar em uma folha que identificará essa amostra como uma flor do tipo Iris-versicolor.
Figura 6: Percorrendo o dataset para encontrar a classe Iris-versicolor, como mostrado na Figura 6.
Agora mais uma amostra com as características:
| SepalLength | SepalWidth | PetalLength | PetalWidth |
|---|---|---|---|
| 7.0 | 3.2 | 5.2 | 2.4 |
Podemos classificar essa flor como uma Iris-virginica, como mostrado na Figura 7.
Figura 7: Percorrendo o dataset para encontrar a classe Iris-virginica.
A Decision Tree possui uma estrutura que pode ser facilmente interpretada, porque podemos a partir de uma amostra percorrer seus nós de condições até chegar em uma folha que identifica a classe dessa amostra. Mas como funciona a criação desses nós de condições?
Entendendo como funciona a Decision Tree
Entropia
Para montar uma Decision Tree é necessário saber quais valores separam melhor os dados, e a entropia é utilizada para calcular a incerteza dos dados, então este valor representa a quantidade das amostras das várias classes.
Quando mais próximo for o valor de zero, menor será a variação das classes, portanto teremos mais amostras da mesma classe, e o contrário indica que os dados possuem amostras de várias classes.
A entropia dos dados é calculada com a Equação 1:
Equação 1: Equação da Entropia.
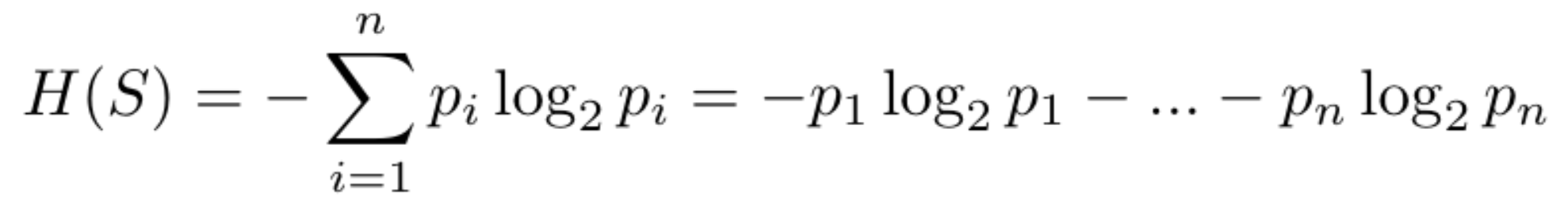
Cada p representa a probabilidade de uma amostra ser de uma determinada classe.
No primeiro Nó da árvore temos a entropia com valor 1.585, e isso representa uma entropia alta, porque neste momento temos amostra de dados das três classes de Iris.
Figura 8: Primeiro nó da Decision Tree treinada com o dataset de flores Iris.

Para calcular a entropia, primeiro calculamos a probabilidade de cada classe. Dado que temos 150 amostras e se você olhar o dataset conseguirá identificar que há 50 amostras de cada classe, as probabilidades desse dataset serão iguais para todos três tipos de Iris:
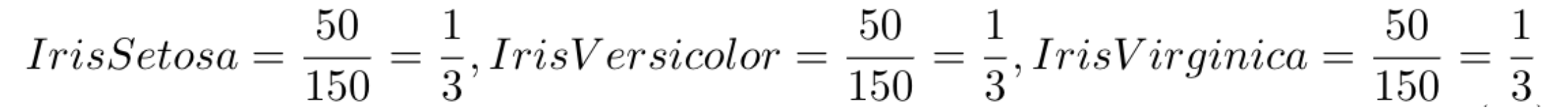
Depois calculamos o valor da entropia:
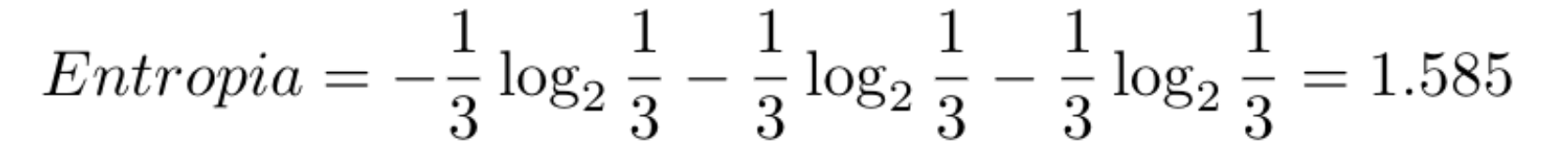
A identificação da condição que separa os dados varia de acordo com a implementação da árvore, mas uma forma básica de obter essa condição é por meio de uma função que testa para cada característica, se essa característica possui um valor que melhor consegue separar os exemplos.
Na primeira folha da árvore (que podemos chegar a partir do nó inicial) temos a entropia de 0.0, que representa uma entropia baixa, porque neste momento temos amostra de apenas uma classe. Então podemos dizer que a condição obtída no primeiro nó é muito boa, porque conseguiu isolar completamente um tipo de Iris com base em um valor da característica SepalLength.
Figura 9: Primeiro nó da Decision Tree treinada com o dataset de flores Iris.

Se calcularmos a probabilidade de cada classe, dado que temos apenas 50 amostras e todas são da classe Iris Setosa, as probabilidades são:
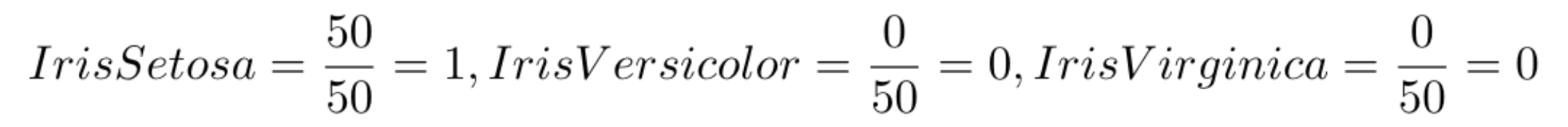
Depois calculamos o valor da entropia:
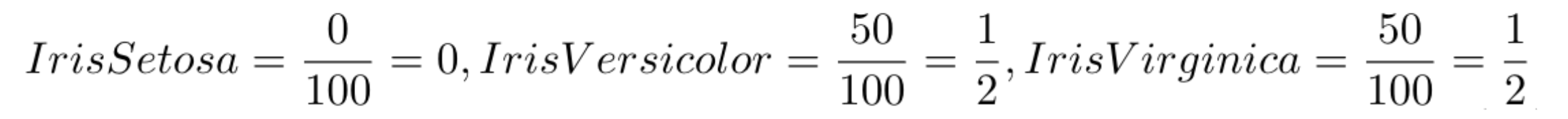
No segundo Nó da árvore temos a entropia de 1.0, que representa uma entropia alta, porque neste momento ainda temos amostra de duas classes.
Figura 10: Primeiro nó da Decision Tree treinada com o dataset de flores Iris.

Calculamos a probabilidade de cada classe. Dado que temos 100 amostras e 50 são da classe Iris Versicolor e 50 são da classe Iris Virginica, as probabilidades são:
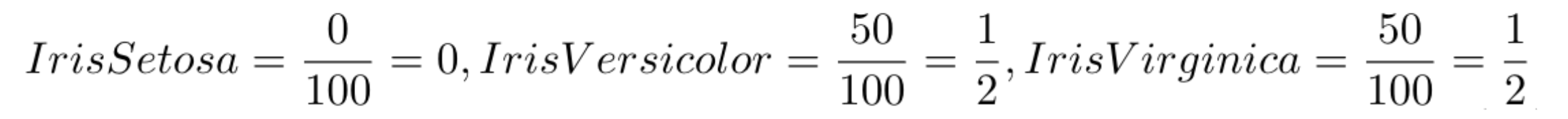
Depois calculamos o valor da entropia:
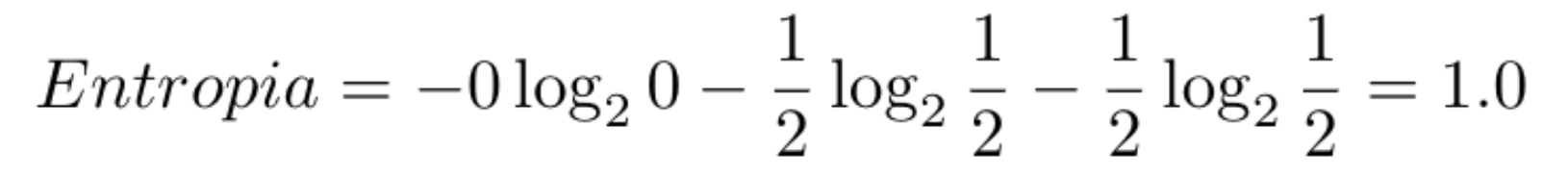
E assim por diante, até chegar no nível de profundidade máxima da árvore. Mas qual é o nível de profundidade máxima da árvore?
Quando treinamos uma Decision Tree, precisamos definir um valor de k que representa a profundidade máxima da árvore, para a identificação desse valor é feita a partir de experimentações do treino com base no dataset, não tem um valor que é bom para treinar qualquer Decision Tree independente do dataset. Se for um valor muito baixo pode não separar bem todas as classes, e se for um valor muito alto pode classificar muito bem o dataset de treino, mas que ao receber valores um pouco diferentes já não conseguirá mais acertar a classificação (isso é chamado de overfitting).
Implementando o calculo da entropia
Se você não está familiarizado com equações matemáticas, como da entropia:
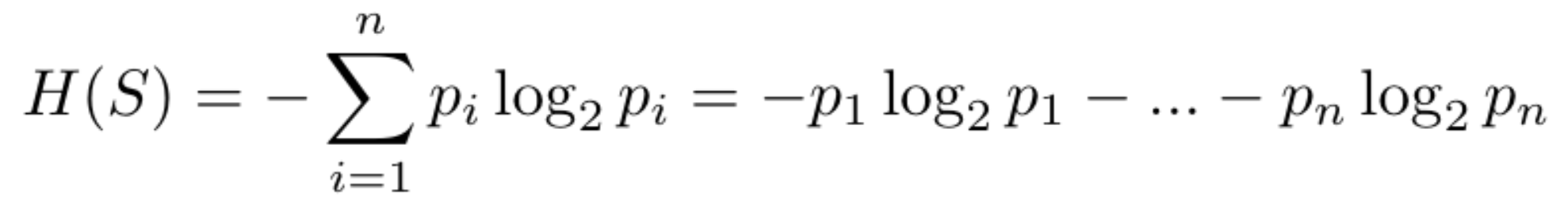
Pode ter pensado, não preciso saber implementar isso, por que hoje em dia já tem disponível em algum lugar já implementado, mas só para mostrar que a equação não é nenhum bixo de sete cabeças, a sua implementação em Java e Python é assim:
Java:
1
2
3
4
5
public double entropia(double ... probabilidades) {
return Arrays.stream(probabilidades)
.map(p -> (p > 0.0) ? (-p * (Math.log(p) / Math.log(2.0))) : 0.0)
.sum();
}
Python:
1
2
def entropia(probabilidades):
return sum(-p * math.log(p, 2) for p in probabilidades if p)
Você tem uma somatoria da negação de cada probabilidade multiplicado pelo log dessa probabilidade.
Então com base no dataset você pode contar quantos exemplos possui representando cada classe e calcular a probabilidade que será passada para o cálculo da entropia:
Java:
1
2
3
4
double p1 = 50.0 / 150.0;
double p2 = 50.0 / 150.0;
double p3 = 50.0 / 150.0;
System.out.println(entropia(p1, p2, p3));
Python:
1
2
3
4
p1 = 50.0/150.0
p2 = 50.0/150.0
p3 = 50.0/150.0
print(entropia([p1, p2, p3]))
Saída:
1
1.584962500721156
Mas continuando, vamos ver como usar uma biblioteca que já possui a Decision Tree implementada.
Usando Smile e Scikit-learn para treinar uma Decision Tree em Java e Python
No Java e Python, temos várias bibliotecas implementadas que facilitam o uso de modelos de aprendizado de máquinas:
Carregando o Dataset de Iris
Você pode fazer o download do dataset de Iris Dataset baixando apenas o arquivo iris.data.
Para carregar esse arquivo separando os valores da classe, podemos implementar uma classe em Java para isso, similar a seguinte:
Java:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
public class Dataset {
private double[][] X;
private int[] y;
private int posicao = 0;
private List<String> classes = new ArrayList();
public Dataset(String filePath) throws IOException {
Path path = Paths.get(filePath);
int exemplos = (int) Files.lines(path).count();
X = new double[exemplos][];
y = new int[exemplos];
Files.lines(path).map(linha -> linha.split(",")).forEach(colunas -> add(colunas));
}
private void add(String[] colunas) {
if (colunas.length > 1) {
double[] Xi = new double[colunas.length - 1];
for (int i = 0; i < colunas.length - 1; i++) {
Xi[i] = Double.valueOf(colunas[i]);
}
X[posicao] = Xi;
if (!classes.contains(colunas[colunas.length - 1])) {
classes.add(colunas[colunas.length - 1]);
}
y[posicao] = classes.indexOf(colunas[colunas.length - 1]);
posicao++;
}
}
public double[][] getX() {
return X;
}
public int[] getY() {
return y;
}
public List<String> getClasses() {
return classes;
}
}
O construtor da classe Dataset recebe um caminho de arquivo, lê esse arquivo e separa os valores em uma matrix X com as caracteristicas e um vetor y com a classe. Importante que o arquivo separe os valores usando virgula e que a classe fique na última coluna, mas isso também é algo que podemos alterar essa classe para ter um suporte melhor.
Nos algoritmos a classe (Versicolor, Setosa e Virginica) converti para um número inteiro, que na verdade representa em qual posição da lista guardei o nome da classe. Deixei também um get da lista de Strings para depois de obter a classificação pegar o texto que representa a classe.
Para usar essa classe e obter os dados do arquivo iris.data:
Java:
1
2
3
4
5
6
Dataset dataset = new Dataset("caminho_dataset/iris.data");
// Definimos uma matriz "X" com as caracteristicas que representam uma flor Iris.
double[][] X = dataset.getX();
// E um vetor "y" com das classes de cada uma das flores.
int[] y = dataset.getY();
No Python temos o Pandas, podemos carregar facilmente os dados a partir de um dataset como um arquivo CSV. Informamos qual o path do dataset e também quais são as características desse dataset. Passamos essas características porque esse dataset não possui um cabeçalho com o nome das colunas.
Python:
1
2
3
4
5
6
7
8
9
import pandas as pd
atributos = ['SepalLength', 'SepalWidth', 'PetalLength', 'PetalWidth', 'Class']
df = pd.read_csv('iris.data', names=atributos)
# Definimos uma matriz "X" com as caracteristicas que representam uma flor Iris.
X = df[df.columns.difference(['Class'])].values
# E um vetor "y" com das classes de cada uma das flores.
y = df['Class'].values
Treinando uma Decision Tree
No Java podemos usar o Smile que possui uma versão implementada da Decision Tree. Costumo importar a dependência via Maven:
1
2
3
4
5
<dependency>
<groupId>com.github.haifengl</groupId>
<artifactId>smile-core</artifactId>
<version>1.5.3</version>
</dependency>
Mas se preferir pode fazer download do jar e colocar nas dependências do projeto.
Java:
1
2
3
4
5
6
Dataset dataset = new Dataset("/Users/rafaelsakurai/Documents/blog/Blog/src/main/resources/iris.data");
double[][] X = dataset.getX(); // Entradas
int[] y = dataset.getY(); // Saída esperada
// Quando criamos uma DecisionTree ela já é treinada com os dados passados em X e y.
DecisionTree tree = new DecisionTree(X, y, 3, DecisionTree.SplitRule.ENTROPY);
No Python temos o Scikit que também tem um Decision Tree, que podemos criar explicitando o tipo de critério que queremos utilizar para gerar os nós de decisão e também a profundidade máxima da árvore gerada.
Python:
1
2
3
4
5
6
7
8
from sklearn.tree import DecisionTreeClassifier
iris_classificador = DecisionTreeClassifier(random_state=1234, criterion='entropy', max_depth=3)
# A função fit é usada para treinar o modelo, com base nas entradas X
# ('SepalLength', 'SepalWidth', 'PetalLength', 'PetalWidth') deve
# aprender a classificar y ('Class').
iris_classificador.fit(X, y)
Após treinar o modelo, podemos passar novas amostras que esse modelo não conhece para ver se ele está conseguindo classificar corretamente.
Predizendo novas amostras
Com o modelo treinado, agora queremos tentar predizer os novos exemplos.
Java:
1
2
3
4
5
6
double[][] novos_exemplos = new double[][]{ {5.0, 3.6, 1.6, 0.5}, {5.8, 2.7, 4.2, 1.2}, {7.0, 3.2, 5.2, 2.4} };
for (double[] novo : novos_exemplos) {
// O método predict classifica novos exemplos de amostras.
int predicao = tree.predict(novo);
System.out.println(Arrays.toString(novo) + " = " + dataset.getClasses().get(predicao));
}
Saída:
1
2
3
[5.0, 3.6, 1.6, 0.5] = Iris-setosa
[5.8, 2.7, 4.2, 1.2] = Iris-versicolor
[7.0, 3.2, 5.2, 2.4] = Iris-virginica
Python:
1
2
3
4
novos_exemplos = [[1.6, 0.5, 5.0, 3.6], [4.2, 1.2, 5.8, 2.7], [5.2, 2.4, 7.0, 3.2]]
# Função predict classificar novos exemplos de amostras.
print(iris_classificador.predict(novos_exemplos))
Saída:
1
['Iris-setosa' 'Iris-versicolor' 'Iris-virginica']
Uma forma bem utilizada para avaliar como está a classificação dessa Decision Tree é por meio da Validação Cruzada, mas depois vou montar um post só falando sobre validação de modelos.
Avaliando a Decision Tree com validação cruzada
A validação cruzada é uma forma de tentar avaliar o quanto seu modelo está conseguindo aprender a classificar os dados. A ideia é dividir o dataset em n partes iguais e para cada uma das n partes, esconde uma parte para teste e usa as demais para treino.
Nesse exemplo, vou dividir o dataset em 5 partes, por tanto cada parte terá 20 amostras do dataset, então a validação cruzada vai pegar uma dessas partes com 20 amostras e guardar para usar no teste e usar 80 amostras para treinar o Decision Tree. Isso será feito 5 vezes, uma para cada parte, e no final imprime a média do resultado do teste de cada parte.
Python:
1
2
3
from sklearn.model_selection import cross_val_score
avaliacao = cross_val_score(iris_classificador, X, y, scoring='accuracy', cv=5)
print(avaliacao.mean())