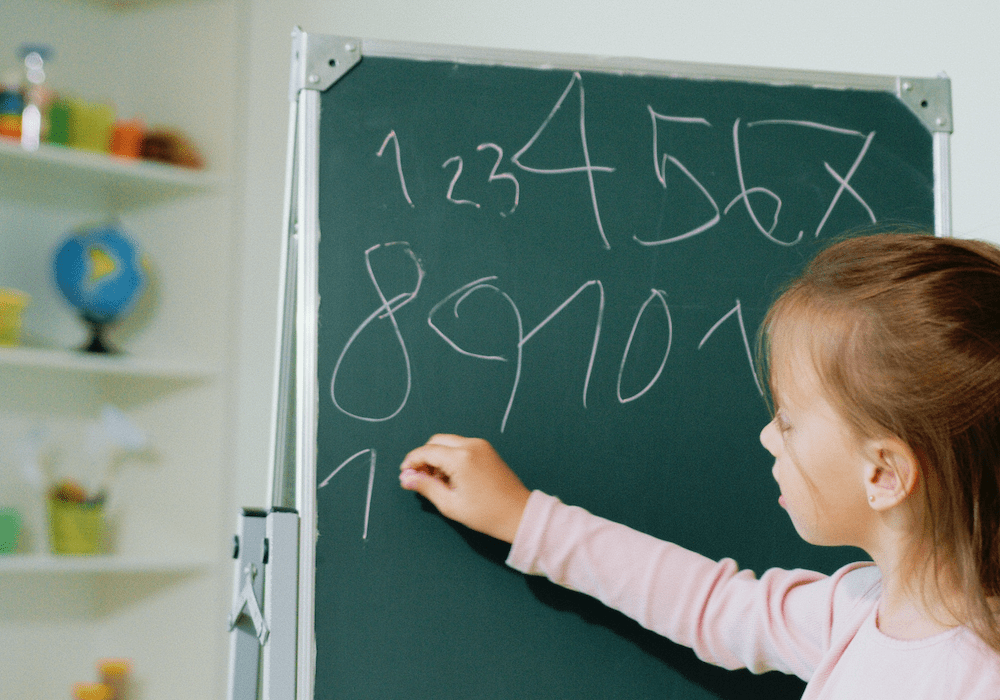
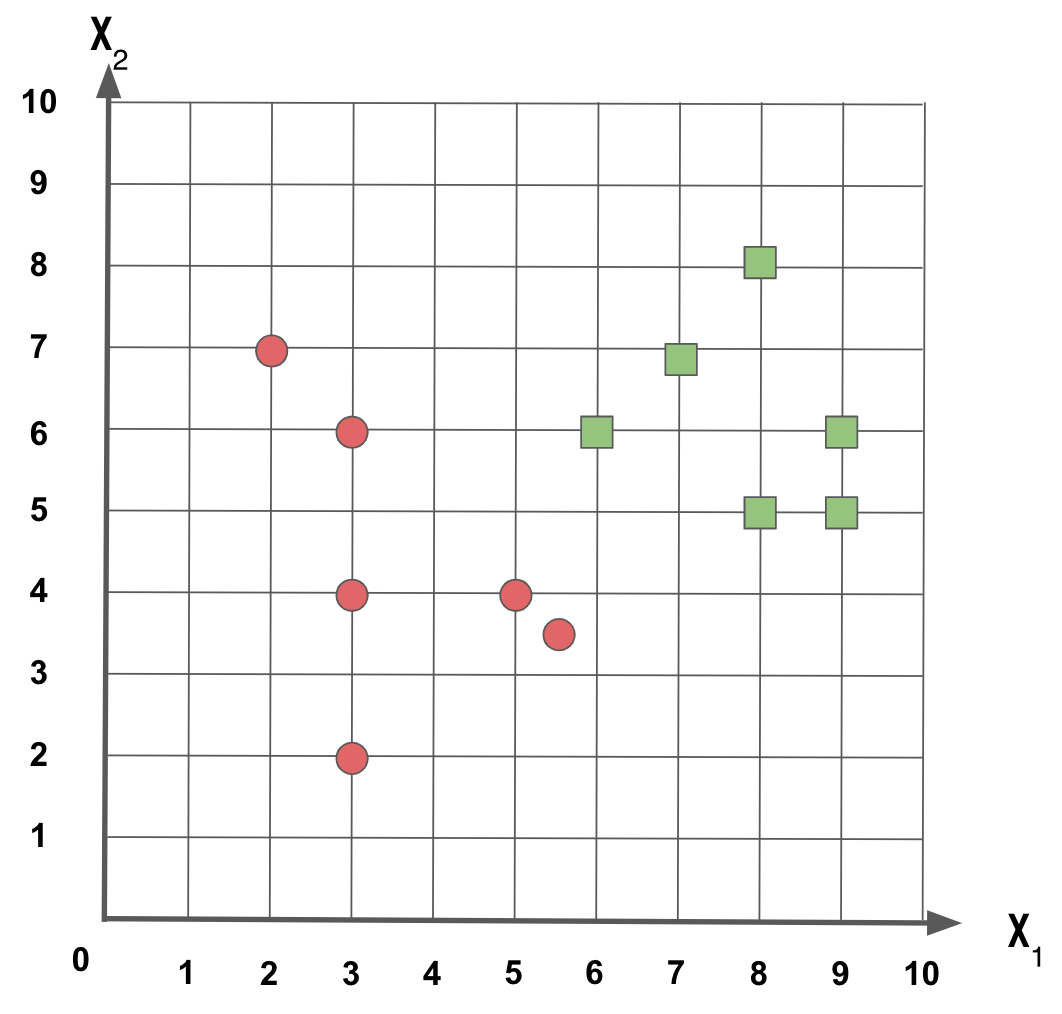
Dado que temos um conjunto de dados composto por amostras com as características x e y, e representada pelas classes círculo vermelho e quadrado verde, como mostrado na Figura 1, como podemos separar as duas classes dos exemplos?

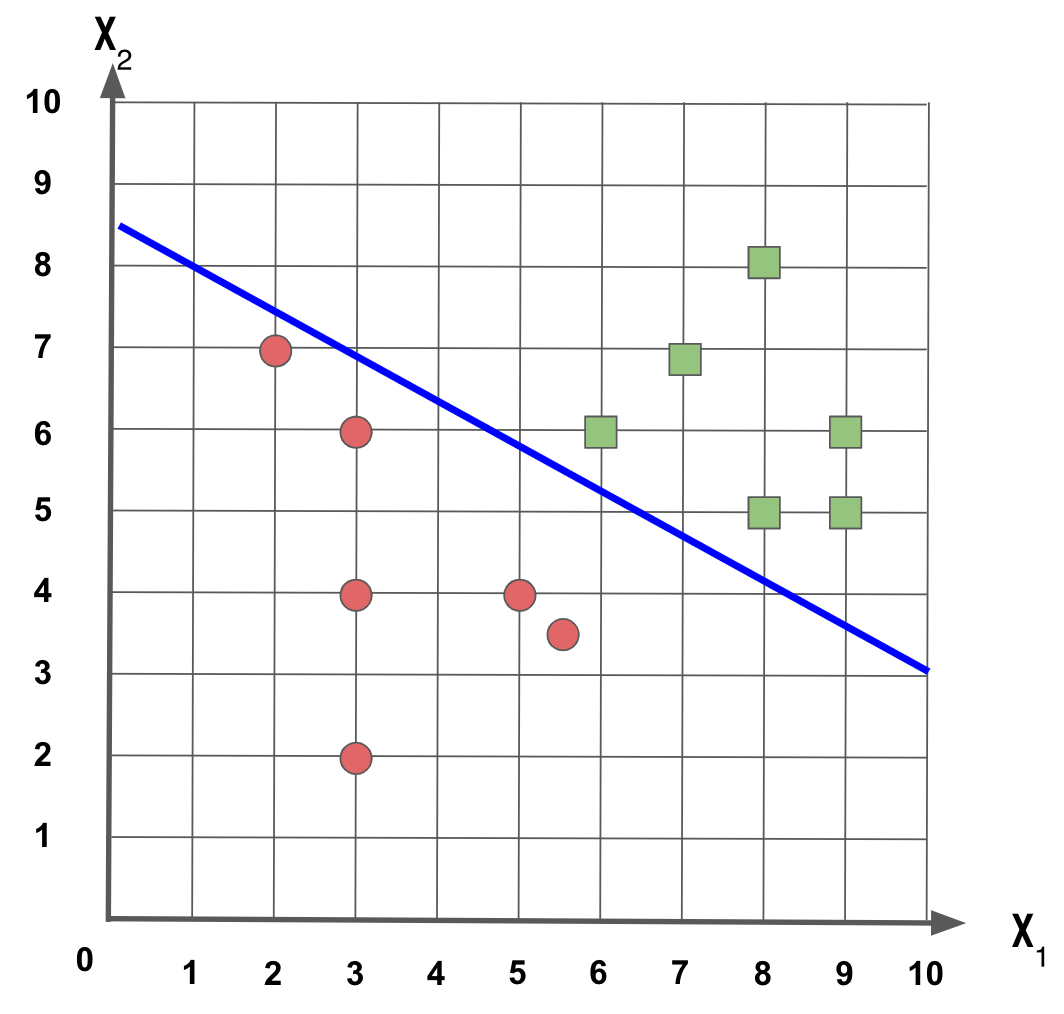
Podemos fazer traçar uma linha que linearmente separa as duas classes, assim:

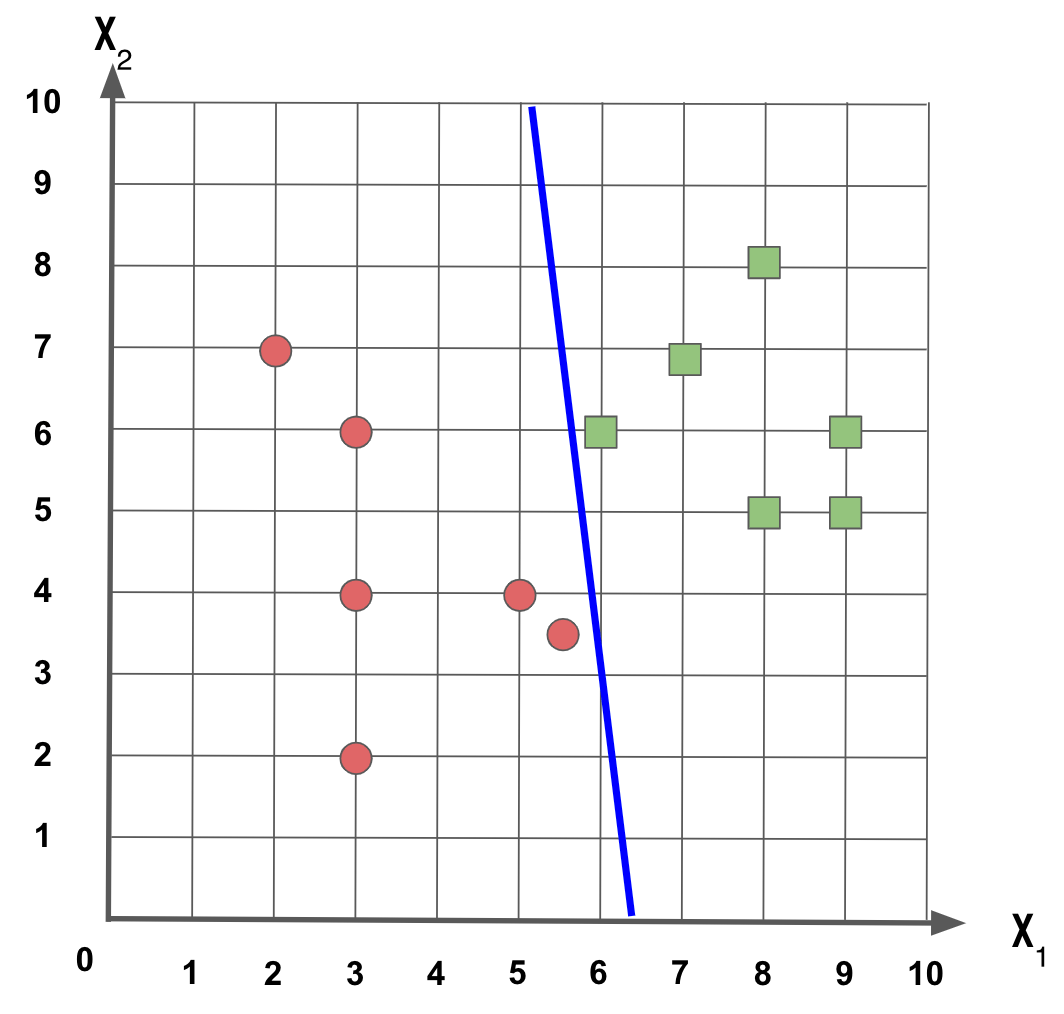
Se fizermos esta outra reta, obtemos um resultado melhor?

E se a reta for igual a mostrada na Figura 4, fica melhor?

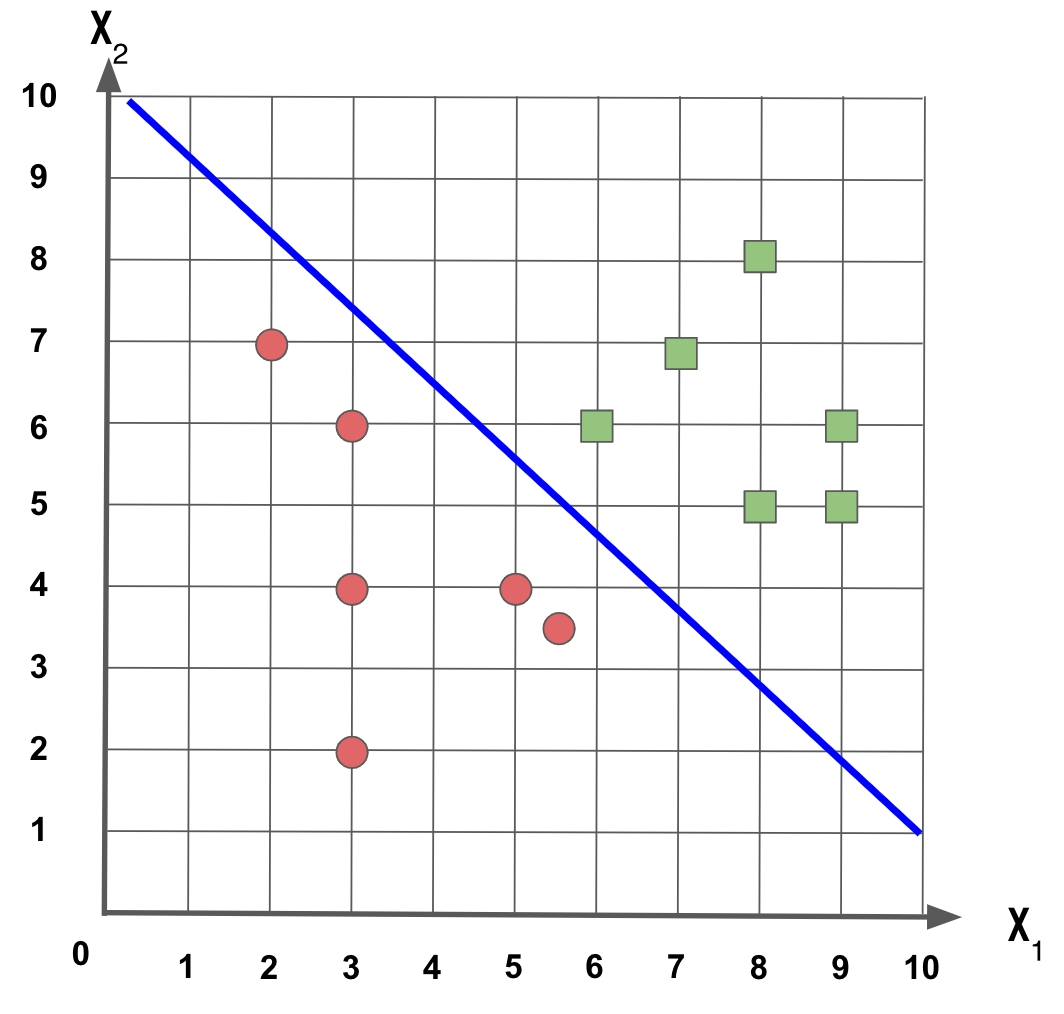
Qual destas três retas melhor separa esse conjunto de dados?

Neste exemplo, as três retas fazem sentido e conseguem separar os dois conjuntos de dados. Mas podemos gerar uma reta que melhor faz isso? Vejamos o que é o Support Vector Machine (SVM) e como ele ajuda nessa tarefa.

A Máquina de Vetores de Suporte (SVM) tem como objetivo criar hiperplanos que melhor separam as classes.

A ideia do SVM é que a melhor reta (hiperplano) é aquela que maximiza a distância entre as classes.

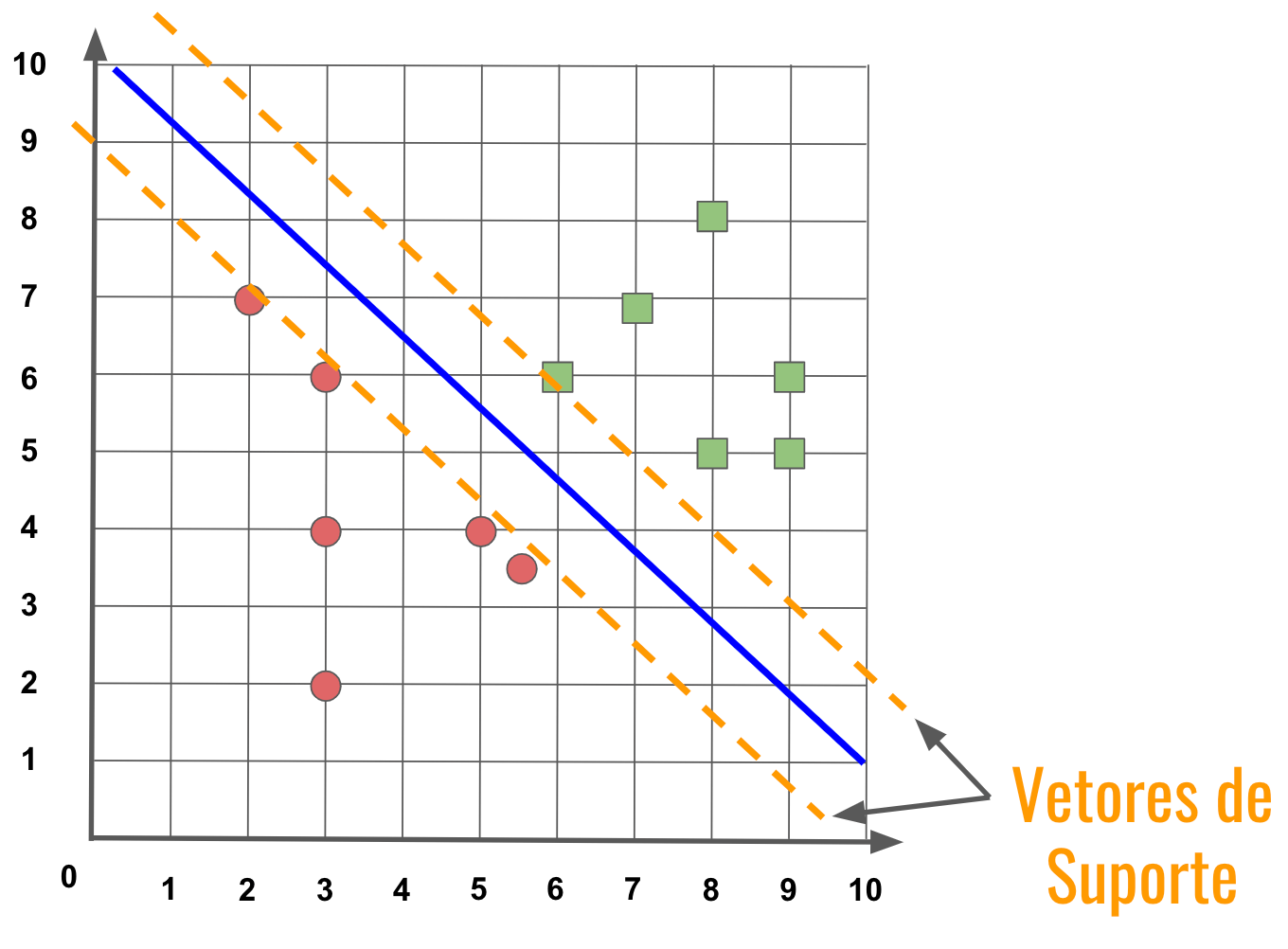
Quanto maior a margem que separa as classes, melhor será o classificador.

Exemplo de classificação de dígitos usando o SVM

Neste exemplo vamos classificar dígitos escritos manualmente, o Dataset Optical Recognition of Handwritten Digits possui um conjunto de dígitos que foram escritos a mão e digitalizados. Cada dígito é representado como uma matriz 8x8, totalizando 64 valores, e cada valor dessa matriz varia em uma escala de 0 a 16, sendo 0 a cor branca e 16 a cor preta.

Então comparando com o exemplo inicial que tem apenas duas características, agora neste exemplo temos 64 características, por tanto 64 eixos e o que o SVM vai fazer é tentar encontrar entre as margens entre os eixos que melhor vão separar os dígitos.

O Scikit-Learn possui este dataset na sua biblioteca, então para facilitar vamos verificar os valores que compõem os dígitos deste dataset:

1
2
3
4
from sklearn import datasets

digitos = datasets.load_digits()
print(digitos.data)

O digitos é um objeto do tipo Bunch que é um utilitário do Scikit, em cada registro temos um exemplo de dígito:

1
2
3
4
5
6
7
8
<class 'sklearn.utils.Bunch'>
[[ 0.  0.  5. ...  0.  0.  0.]
 [ 0.  0.  0. ... 10.  0.  0.]
 [ 0.  0.  0. ... 16.  9.  0.]
 ...
 [ 0.  0.  1. ...  6.  0.  0.]
 [ 0.  0.  2. ... 12.  0.  0.]
 [ 0.  0. 10. ... 12.  1.  0.]]

Outra forma de visualizar esses dados é fazendo um plot para ter uma ideia visual de como são esses dígitos, vamos gerar uma imagem com os primeiros dez dígitos:

1
2
3
4
5
6
7
8
import matplotlib.pyplot as plt

fig, axs = plt.subplots(2, 5, figsize=(12, 5))

for i in range(0, 2):
  for j in range(0, 5):
    axs[i, j].imshow(digitos.images[(i * 5) + j], cmap=plt.cm.gray_r, interpolation="nearest")
plt.show()

Temos como resultado:

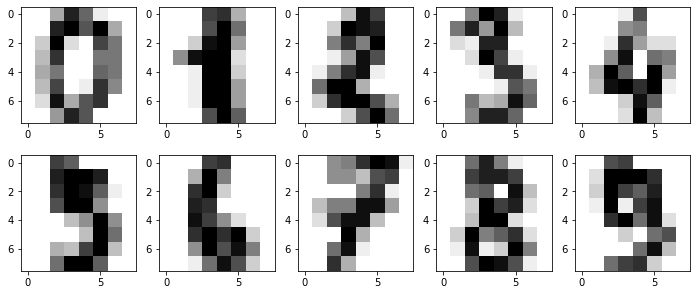
Olhando a imagem de cada número podemos ver alguns números que apresentam menos cores (1 e 6) e mais cores (0, 2, e 8) e vemos números similares (3, 5 e 9).

Agora vamos ler o Dataset Optical Recognition of Handwritten Digits, nele temos um arquivo de treino e outro de teste. Vamos começar lendo o arquivo de treino e pegando apenas as primeiras 64 características de cada linha, isso porque a última característica é o número do dígito que queremos aprender a classificar.

1
2
3
4
5
import pandas as pd

df_treino = pd.read_csv('optdigits_treino.csv', header=None)
X_treino = df_treino.loc[:,0:63]
print(X_treino)

Aqui temos alguns exemplos dos dados, para cada linha representando um dígito, temos 64 características com o valor que representa a cor preenchida naquela posição.

1
2
3
4
5
6
7
8
9
10
11
12
     0   1   2   3   4   5   6   7   8   ...  55  56  57  58  59  60  61  62  63
0      0   1   6  15  12   1   0   0   0  ...   0   0   0   6  14   7   1   0   0
1      0   0  10  16   6   0   0   0   0  ...   0   0   0  10  16  15   3   0   0
2      0   0   8  15  16  13   0   0   0  ...   0   0   0   9  14   0   0   0   0
3      0   0   0   3  11  16   0   0   0  ...   0   0   0   0   1  15   2   0   0
4      0   0   5  14   4   0   0   0   0  ...   0   0   0   4  12  14   7   0   0
...   ..  ..  ..  ..  ..  ..  ..  ..  ..  ...  ..  ..  ..  ..  ..  ..  ..  ..  ..
3818   0   0   5  13  11   2   0   0   0  ...   0   0   0   8  13  15  10   1   0
3819   0   0   0   1  12   1   0   0   0  ...   0   0   0   0   4   9   0   0   0
3820   0   0   3  15   0   0   0   0   0  ...   0   0   0   4  14  16   9   0   0
3821   0   0   6  16   2   0   0   0   0  ...   0   0   0   5  16  16  16   5   0
3822   0   0   2  15  16  13   1   0   0  ...   0   0   0   4  14   1   0   0   0

Vamos agora separar apenas a última característica de cada linha que é o valor do dígito, a classe que o modelo deve aprender.

1
2
y_treino = df_treino.loc[:,64]
print(y_treino)

1
2
3
4
5
6
7
8
9
10
11
12
13
[3823 rows x 64 columns]
0       0
1       0
2       7
3       4
4       6
       ..
3818    9
3819    4
3820    6
3821    6
3822    7
Name: 64, Length: 3823, dtype: int64

Agora que já conhecemos os dados, vamos treinar um SVM para classificar os dígitos com base nos valores das intensidades de cores da forma como cada dígito foi escrito.

O Scikit-Learn possui algumas implementações de SVM vamos usar a versão LinearSVC que é usada para fazer classificação.

Vamos chamar o método fit passando as características de treino e a saída esperada:

1
2
3
4
from sklearn.svm import LinearSVC

modelo = LinearSVC()
modelo.fit(X_treino, y_treino)

Agora vamos carregar os dados de teste para avaliar como ficou o modelo treinado, também vou separar a última coluna que representa a classificação do dígito:

1
2
3
4
5
import pandas as pd

df_teste = pd.read_csv('optdigits_teste.csv', header=None)
X_teste = df_teste.loc[:,0:63]
y_teste = df_teste.loc[:,64]

Vamos classificar os dados de teste e verificar como ficou a acurácia do modelo:

1
2
3
4
from sklearn import metrics

y_predito = modelo.predict(X_teste)
print("Acurácia: {}".format(metrics.accuracy_score(y_teste, y_predito)))

O modelo ficou com uma acurácia boa:

1
Acurácia: 0.9148580968280468

Isso indica que dado o conjunto de teste, o modelo conseguiu classificar corretamente 91% das amostras.

Um ponto importante é que não passei nenhuma configuração personalizada para o treino do modelo, caso você queira, dê uma olhada nos parâmetros que o LinearSVC permite configurar e treine novamente o modelo para tentar obter uma classificação melhor.

Matriz de confusão

Vamos gerar a matriz de confusão para tentar entender como o modelo está classificando as amostras de testes:

1
2
3
from sklearn.metrics import confusion_matrix
matrix = confusion_matrix(y_teste, y_predito)
print(matrix)

Na matriz de confusão é muito importante que a diagonal principal tenha os maiores valores, porque os demais valores indicam com o que uma amostra está sendo confundida:

1
2
3
4
5
6
7
8
9
10
[[173   0   0   0   0   2   0   0   2   1]
 [  0 144   0   0   0   0   0   0  31   7]
 [  0   1 170   0   0   0   0   0   6   0]
 [  1   0   1 157   0   3   0   0  18   3]
 [  0   0   0   0 175   0   0   1   4   1]
 [  0   0   1   1   0 172   0   0   6   2]
 [  0   0   0   0   2   0 172   0   7   0]
 [  0   0   0   0   2   7   0 160   2   8]
 [  0   3   0   0   0   1   0   0 168   2]
 [  0   1   0   1   5   1   0   1  18 153]]

Podemos também gerar uma versão gráfica da matriz de confusão:

1
2
3
from sklearn.metrics import ConfusionMatrixDisplay
disp = ConfusionMatrixDisplay(confusion_matrix=matrix, display_labels=['0', '1', '2', '3', '4', '5', '6', '7', '8', '9'])
disp.plot();

Conseguimos identificar que os números 1 e 4 são mais confundidos com o número 8:

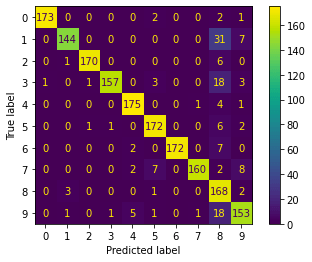
Mas o importante é que está conseguindo classificar corretamente a maioria das amostras de cada dígito.