Implementando a estrutura de uma Rede Neural Convolucional utilizando o MapReduce do Spark
A classificação de imagens é uma tarefa na qual dada uma figura é obtido uma saída que representa sua classe (rótulo) ou a probabilidade das classes que descrevem a figura. Neste documento é apresentado um exemplo de problema que pode ser tratado por meio de Redes Neurais Convolucionais sendo implementado utilizando a técnica de MapReduce do Spark.
Rede Neural Convolucional
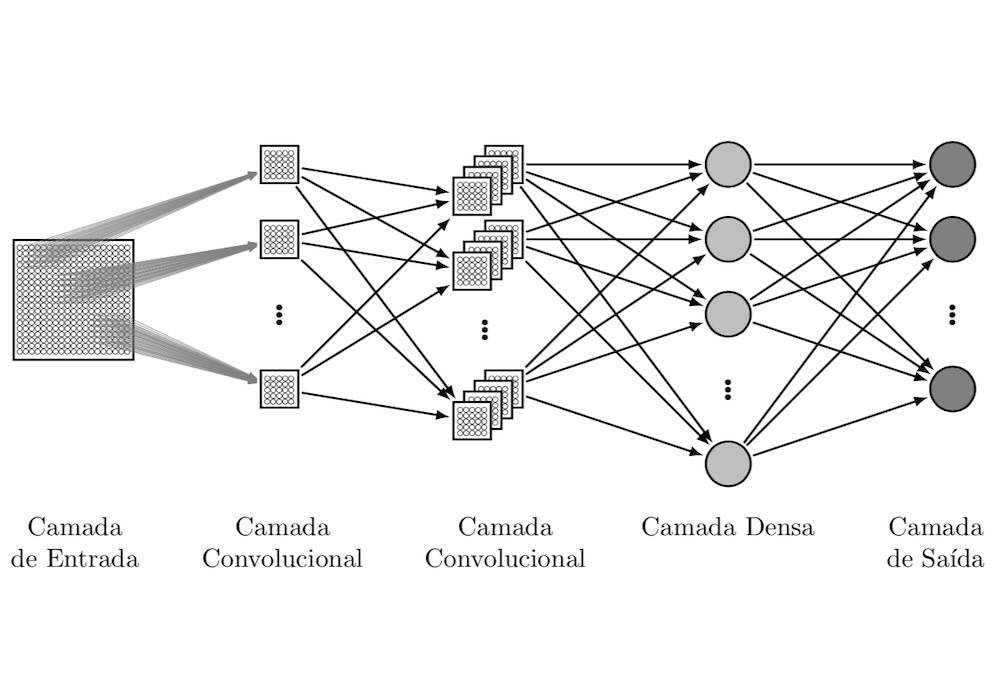
A Rede Neural Convolucional (do inglês Convolutional Neural Network - CNN) vem ganhando destaque na classificação de imagens. A Figura 1 apresenta um exemplo de arquitetura de CNN.
Figura 1: Exemplo de topologia da Rede Neural Convolucional.

O diferencial das CNNs está nas diversas camadas convolucionais, que aplica uma função matemática de Convolução nos dados de entrada e depois realizando o Agrupamento (pooling). A saída da convolução é passada para a próxima camada convolucional até chegar na última camada conhecida como Camada Densa que normalmente é representada por uma rede Perceptron de múltiplas camadas (do inglês Multilayer Perceptron - MLP).
Conjunto de dados de treino
A biblioteca scikit-learn possui internamente um conjunto de dados composto por 1.797 exemplos de imagens de dígitos 0 à 9.
Neste conjunto de dados estão disponíveis os dígitos e sua classe, como apresentado na Figura 2. Cada dígito é formado por uma matriz de dimensão de 8 x 8, como mostrado na Tabela 1.
1
2
3
4
5
6
7
8
9
10
11
12
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
digits = load_digits()
plt.figure(figsize=(20,4))
for index, (image, label) in enumerate(zip(digits.data[0:5], digits.target[0:5])):
plt.subplot(1, 5, index + 1)
plt.imshow(np.reshape(image, (8,8)), cmap=plt.cm.gray)
plt.title('Training: %i\n' % label, fontsize = 20)
plt.show()
Figura 2: Exemplo dos dígitos utilizados no treinamento.

Tabela 1: Matriz de dimensão 8 x 8 com os valores que correspondem ao exemplo de um dígito zero.
1
print(np.reshape(digits.data[0], (8, 8)))
| 0.0 | 0.0 | 5.0 | 13.0 | 9.0 | 1.0 | 0.0 | 0.0 |
| 0.0 | 0.0 | 13.0 | 15.0 | 10.0 | 15.0 | 5.0 | 0.0 |
| 0.0 | 3.0 | 15.0 | 2.0 | 0.0 | 11.0 | 8.0 | 0.0 |
| 0.0 | 4.0 | 12.0 | 0.0 | 0.0 | 8.0 | 8.0 | 0.0 |
| 0.0 | 5.0 | 8.0 | 0.0 | 0.0 | 9.0 | 8.0 | 0.0 |
| 0.0 | 4.0 | 11.0 | 0.0 | 1.0 | 12.0 | 7.0 | 0.0 |
| 0.0 | 2.0 | 14.0 | 5.0 | 10.0 | 12.0 | 0.0 | 0.0 |
| 0.0 | 0.0 | 6.0 | 13.0 | 10.0 | 0.0 | 0.0 | 0.0 |
Aplicando Redes Neurais Convolucionais para classificação dos dígitos
Neste exemplo será apresentado o uso da CNN para a partir dos dados do dígitos tentar classificá-lo.
Realizando a convolução
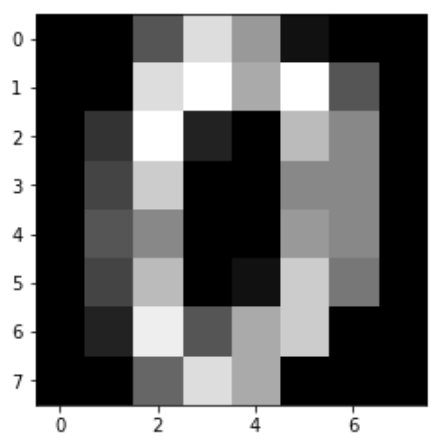
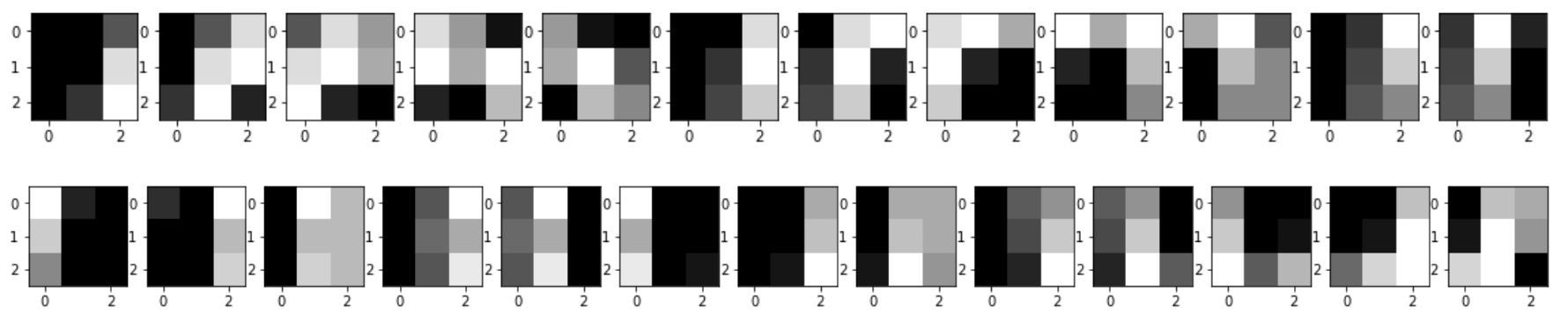
Com base na entrada, por exemplo o digito zero representado na Figura 3, pode ser aplicado um mapeamento para gerar diversar partes com tamanho igual ao do kernel, como mostrado na Figura 4.
1
2
3
4
5
plt.figure(figsize=(20,4))
for index, (image, label) in enumerate(zip(digits.data[0:1], digits.target[0:5])):
plt.subplot(1, 1, index + 1)
plt.imshow(np.reshape(image, (8,8)), cmap=plt.cm.gray)
plt.show()
Figura 3: Exemplo do dígito zero.
1
2
3
4
5
plt.figure(figsize=(20, 4))
for index, image in enumerate(partesDigito[0][1]):
plt.subplot(1, len(partesDigito[0][1]), index + 1)
plt.imshow(image, cmap=plt.cm.gray)
plt.show()
Figura 4: Exemplo de partes que podem ser geradas a partir do dígito zero.
A convolução é aplicada por meio da Equação 1.
Equação 1: Equação do calculo da convolução.
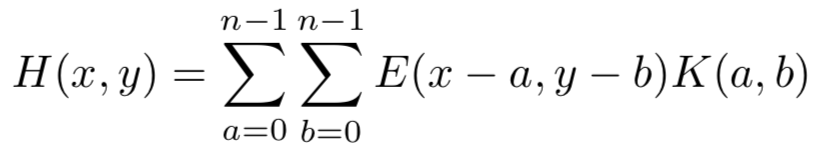
em que dado uma entrada E e um kernel K de dimensão n x n, é somado o resultado da multiplicação de cada posição do kernel por uma área correspondente a partir da posição x e y da entrada, obtendo como resultado uma resposta de ativação.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
en = 8 # tamanho da dimensão da entrada
kn = 3 # tamanho da dimensão do kernel
k = 10 # quantidade de kernels
qtdMatrizes = (en - kn) ** 2
kernels = np.random.randn(k, kn, kn)
def partes(x):
partesDigito = []
entrada = np.zeros(((en - kn) ** 2, kn, kn))
X = x.reshape(en, en) # Muda a entrada vetorial para matriz
for ki in range(0, k): # Para cada kernel separa a entrada em partes
index = 0;
for i in range(0, en - kn):
for j in range(0, en - kn):
entrada[index] = X[i:i+kn, j:j+kn] # Cada parte é uma submatriz da entrada
index += 1
partesDigito.append((ki, entrada)) # Para cada kernel gera varias partes da entrada
return partesDigito
partesDigito = partes(digits.data[0])
print(partesDigito[0])
Saída:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
(0, array([[[ 0., 0., 5.],
[ 0., 0., 13.],
[ 0., 3., 15.]],
[[ 0., 5., 13.],
[ 0., 13., 15.],
[ 3., 15., 2.]],
[[ 5., 13., 9.],
[ 13., 15., 10.],
[ 15., 2., 0.]],
[[ 13., 9., 1.],
[ 15., 10., 15.],
[ 2., 0., 11.]],
...
Após aplicar o kernel em toda área da matriz de entrada, o resultado obtido é um mapa com todas as ativações.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import math
def sigmoid(x):
return 1 / (1 + math.exp(-x))
# t representa a dimensão de um mapa de ativação
t = en - kn + 1
# Aplica a função de ativação no resultado da multiplicação do kernel pela entrada
# Recebe como entrada o kernel e uma matriz com as partes da entrada
def ativacao(k, x):
mapa = np.zeros((t, t)) #Mapa de ativações de um kernel vazio
for i in range(0, len(x) - 1): #Para cada parte da matriz da entrada
mapa[int(i/t)][i%t] = sigmoid((x[i] * k).sum())
return mapa
print("Mapa de ativações de um kernel")
print(ativacao(kernels[0], partesDigito[0][1]))
Saída:
1
2
3
4
5
6
7
Mapa de ativações de um kernel
[[ 0.99998564 0.99999983 0.99999518 1. 1. 0.99999839]
[ 1. 0.99999999 1. 1. 0.99999951 0.99999995]
[ 0.99991458 0.99997446 1. 0.99999991 0.99999982 0.98463398]
[ 0.99995649 0.99999999 0.99999987 1. 0.99908467 0.99998074]
[ 0. 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0. 0. ]]
A Figura 5 apresenta um exemplo visual do que poderia ser a representação visual de um mapa de ativações a partir de dez kernels.
1
2
3
4
5
6
7
8
9
10
mapas = np.zeros((k, t, t))
for i in range(0, k):
mapas[i] = ativacao(kernels[partesDigito[i][0]], partesDigito[i][1])
plt.figure(figsize=(20, 4))
for index, image in enumerate(mapas):
plt.subplot(1, len(mapas), index + 1)
plt.imshow(image, cmap=plt.cm.gray)
plt.show()
Figura 5: Exemplo de mapa de ativações.

Agrupamento com Max Pooling
Após gerado o mapa de ativações é realizado seu agrupamento, normalmente utilizando a função Max Pooling, que agrupa regiões do mapa de ativações mantendo apenas o maior valor de cada região, assim gerando um mapa de ativações mais compacto e mantendo sua principais ativações.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
pn = 2 # tamanho do pooling
ps = 2 # tamanho do passo do pooling
# Max Pooling
def maxPooling(x):
agrupado = np.zeros((int(t / pn), int(t / pn)))
for i in range(0, int(t / pn)):
for j in range(0, int(t / pn)):
agrupado[i][j] = x[i * pn : i * pn + kn - 1, j * pn : j * pn + kn - 1].max()
return agrupado
pooling = []
for i in range(0, len(mapas)):
pooling.append(maxPooling(mapas[i]))
print(pooling[0])
Saída:
1
2
3
4
[[ 1. 1. 1. ]
[ 0.99999999 1. 0.99999982]
[ 0. 0. 0. ]]
Camada densa com Multilayer Perceptron
A cada camada convolucional serão gerados mais mapas de ativações, a última camada convolucional passará os mapas para uma MLP que gera como saída a probabilidade de cada dígito entre 0 e 9 dada a entrada inicial da CNN.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# weights representa os pesos da camada densa (MLP), aqui ainda falta fazer o backpropagation para ajustar esses pesos.
weights = np.random.randn(10, 90)
# função de ativação RELU
def relu(x):
return max(0, x)
# Multilayer Perceptron
def mlp(x):
# A saída é um vetor que será passado para a camada de saída.
saida = []
for w in weights:
saida.append(relu((w * x).sum()))
return saida
print (mlp(np.asarray(pooling).ravel()))
Saída:
1
[0, 0, 0, 4.3701665050961562, 0, 0, 0, 0.60245082809067663, 0, 0, 0.53936137771204695, 12.123892627075183, 5.0597520763051014, 0.27369392536098403, 0, 3.422379266592682, 2.3469559016028905, 0.97873657051551133, 7.7324271328553129, 3.2759378522349918, 2.6000096645266626, 3.6007522524434128, 0, 0, 0, 0, 1.4346841403270592, 0, 1.5324169541119275, 1.378371029334049, 0, 11.142221590259755, 6.5918443871797017, 0, 0, 0, 0, 0, 0.37532997646881272, 0, 2.4526739064332572, 2.9692356615887432, 0.6982483522414773, 1.1695875096513377, 0, 0, 0, 1.7735903055927464, 0, 0, 5.6680899516275787, 3.4132525268346612, 8.5553119395499113, 0, 0, 3.9782447858252392, 0.81613845606182212, 3.727326470346775, 0, 0, 0, 1.7425813090759279, 0, 0, 0, 0, 11.030676379704985, 1.5197188161663346, 7.9210980282255781, 0, 6.4840401213813266, 8.1830919183345063, 0, 0, 0, 5.7380291135098078, 0, 7.6907450104951138, 0, 0.36736327224652277, 0.13878636769635899, 3.90926051261878, 0, 0, 12.233622756093702, 8.5289374934347801, 0.62233906262415628, 0.48997189272927777, 0, 0.54504203418758745, 0.92106676094190298, 0, 0, 4.947342418562382, 1.1909579791507841, 2.8482571182408303, 0, 12.735820503700911, 3.8323855539377258, 2.4634624550847439]
Camada de saída
A camada de saída aplica a função de ativação softmax para gerar uma distribuição de probabilidades entre 0 e 1 nos valores de saída. A saída é um vetor de 10 valores, cada valor representará a probabilidade de que cada um dos números entre zero e nove, tem de representar o número da figura que será classificada.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# weights representa os pesos da camada de saída, aqui ainda falta fazer o backpropagation para ajustar esses pesos.
weightsOut = np.random.randn(10, 1)
# função de ativação SoftMax
def softmax(x):
e_x = np.exp(x - np.max(x))
return e_x / e_x.sum(axis=0)
def out(x):
# A saída representa a probabilidade de cada número entre zero e nove.
saida = []
for i in range(0, len(weightsOut)):
saida.append((weightsOut[i] * x).sum())
return softmax(saida)
x = mlp(np.asarray(pooling).ravel())
print(out(x))
Saída:
1
2
3
[ 3.66082504e-252 2.46136020e-096 2.84453882e-197 5.55449523e-273
2.17623650e-223 2.67780046e-118 8.59637277e-108 1.00000000e+000
2.25062876e-122 6.18347914e-027]
Montando a Rede Neural Convolucional com o MapReduce
A estrutura da CNN é formada por várias camadas que podem ser representadas por meio do mapeamento feito pelo MapReduce do Spark.
Uma forma de representar uma CNN usando MapReduce seria:
- Para cada camada convolucional:
a) Mapeia a entrada para uma matriz com várias partes de tamanho igual ao kernel;
b) Mapeia cada parte da entrada com o kernel, aplicando a função de ativação e gerando um mapa de ativações;
c) Aplica o agrupamento em cada mapa de ativações gerando como saída um mapa de ativações com dimensão reduzida;
d) Junta todos os mapas de ativações, pois serão passados como entrada para a camada seguinte. - A saída da última camada convolucional é passada para uma MLP, que:
a) Mapeia os mapas de ativações para um vetor sequencial;
b) O vetor sequencial é passado para a camada densa que aplica a função de ativação RELU;
c) Os dados são passados para a camada de saída que gera as probabilidades representando cada um dos dígitos.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
sc = SparkContext.getOrCreate()
# Montando um RDD com todo dataset de digitos
rdd = sc.parallelize(digits.data, 4)
# Cria uma matriz com os kernels (filtros) da primeira camada convolucional
kernels1 = np.random.randn(k, kn, kn)
print(rdd
# 1º convolucao
.map(lambda x: partes(x)) # Separa as 25 partes da imagem para cada um dos 10 kernels
.map(lambda x: list(map(lambda y: ativacao(kernels1[y[0]], y[1]), x))) # Gera o mapa de ativações de cada kernel
.map(lambda x: list(map(lambda y: maxPooling(y), x))) # Aplica o max pooling na primeira camada
# Camada Densa (MLP)
.map(lambda x: np.asarray(x).ravel()) # Converte a matriz de saída da camada convolucional para um vetor
.map(lambda x: mlp(x)) # Manda os dados da última camada convolucional agrupada para a camada Densa
.map(lambda x: out(x)) # Aplica o softmax e retorna os valores das probabilidades de cada número.
.take(1))
Saída:
1
2
3
4
[[0.2303787084411721, 0.2099451726892583, 0.06508030989360919,
0.1055256000866959, 0.9971740047740627, 0.09117066280446567,
0.9999356557510007, 1.3844127613072241e-05, 0.8562682290831856,
0.38278995757093703]]
A implementação deste exemplo usando Jupyter Notebook está disponível no GitHub.
Conclusão
A estrutura da Rede Neural Convolucional pode ser aplicada utilizando a técnica de MapReduce, tendo como objetivo paralelizar o processo de convolução e agrupamento. Mas é necessário obter os mapas de ativações gerados por todos os kernels de uma camada convolucional, antes de seguir adiante, pois estes mapas serão a entrada da camada convolucional seguinte. Também é necessário aguardar todos as convoluções paralelas finalizarem para obter a entrada da MLP e após isso, com sua saída, aplicar a retropropagação para ajustar os pesos.