Regressão Linear Múltipla

Quando queremos entender a relação que existe entre mais de duas variáveis quantitativas para tentar predizer um valor, um método que podemos facilmente fazer isso é usando a Regressão Linear Múltipla.
A função da Regressão Linear Múltipla segue o mesmo padrão da Regressão Linear Simples, a diferença é que agora precisamos calcular vários valores de β, sendo um para cada variável que queremos utilizar:
Como: f(x) = α + β₁.x₁ + β₂.x₂ + … + βᵢ.xᵢ
Então se queremos predizer o valor do apartamento, com base na quantidade de metros, vagas de garagem e quantidade de quartos, precisamos calcular três valores de β.
Como: f(valor) = α + β₁ * metros + β₂ * vagas + β₃ * quartos
Neste post, não vou implementar manualmente o cálculo do valor de
αeβ, vou utilizar uma implementação pronta.
Conhecendo o dataset
Seguindo o exemplo de predição do preço do apartamento apresentado no post anterior sobre Regressão Linear Simples. Agora queremos utilizar mais de duas variáveis para predizer qual o preço de um apartamento em SBC.
Coletei de modo aleatório os dados: m², valor, quantidade de quartos, quantidade de vagas de garagem, se o apartamento é novo ou reformado e em qual bairro de SBC está localizado este apartamento, e disponibilizei neste csv.
Estas são as algumas linhas do dataset:
| metros | valor | quartos | vagas | reformado | bairro |
|---|---|---|---|---|---|
| 107 | 560 | 3 | 2 | 0 | Vila Lusitania |
| 49 | 196 | 2 | 1 | 0 | Ferrazopolis |
| 104 | 515 | 3 | 2 | 1 | Centro |
| 51 | 249 | 2 | 1 | 0 | Taboao |
| 50 | 210 | 2 | 1 | 1 | Demarchi |
| 93 | 450 | 3 | 2 | 0 | Baeta Neves |
| 107 | 425 | 3 | 2 | 1 | Rudge Ramos |
No post anterior, foi apresentado como o valor e a quantidade de m² estão correlacionados, mas agora temos outras variáveis, podemos verificar se mais alguma variável também influencia o valor do apartamento.
Olhando a Figura 1, parece que se o apartamento é novo ou se já foi reformado (colocado piso e mobiliado) não influencia o valor do preço do apartamento.
Figura 1: Gráfico de dispersão entre valor e se o apartamento está reformado.
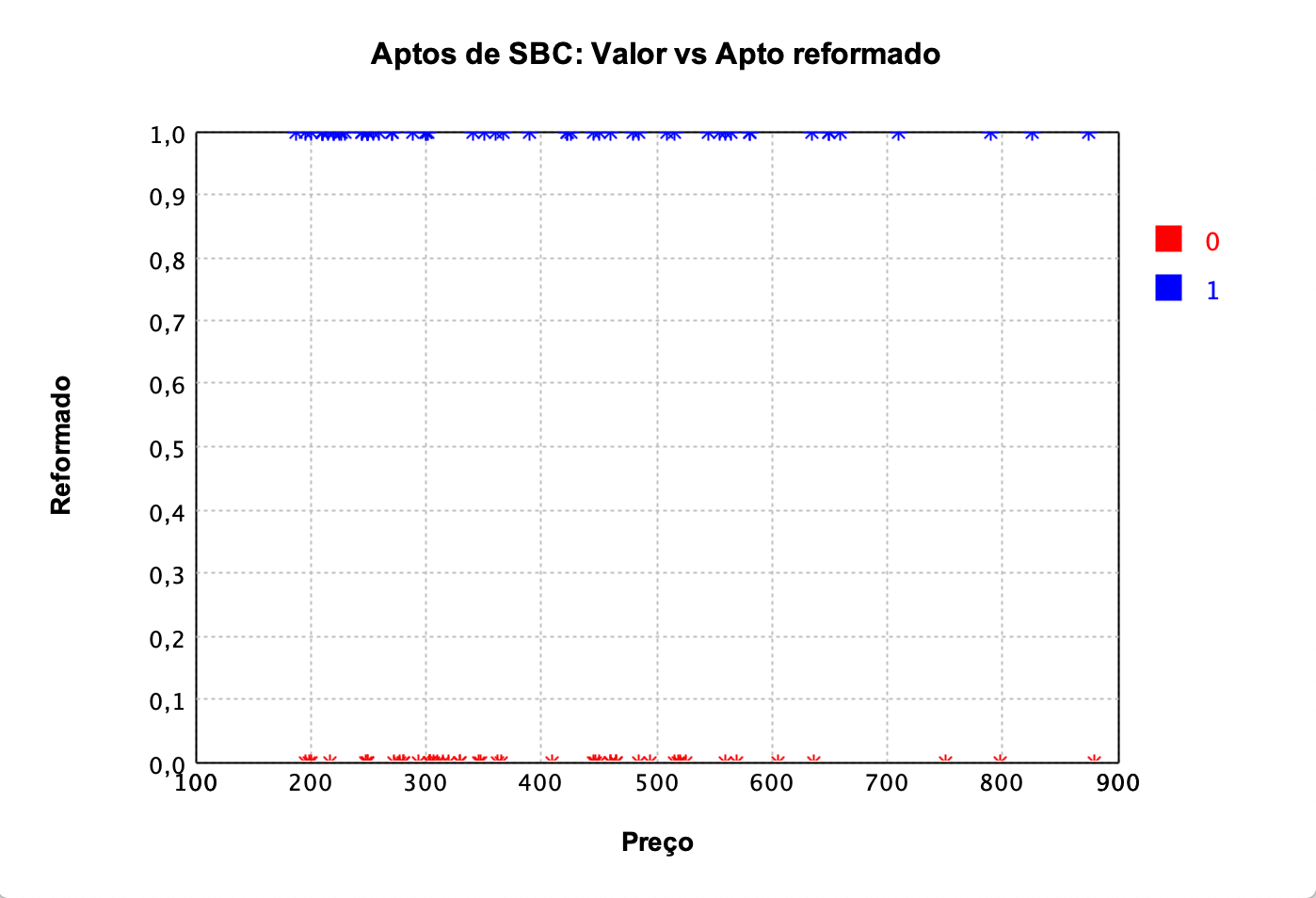
Mas interessante, na Figura 2 e Figura 3 podemos observar que se levarmos em consideração a quantidade de vagas de garagem ou quartos do apartamento, podemos notar que quanto mais, maior será o seu valor.
Figura 2: Gráfico de dispersão entre valor e a quantidade de quartos do apartamento.

Figura 3: Gráfico de dispersão entre valor e a quantidade de vagas de garagem.
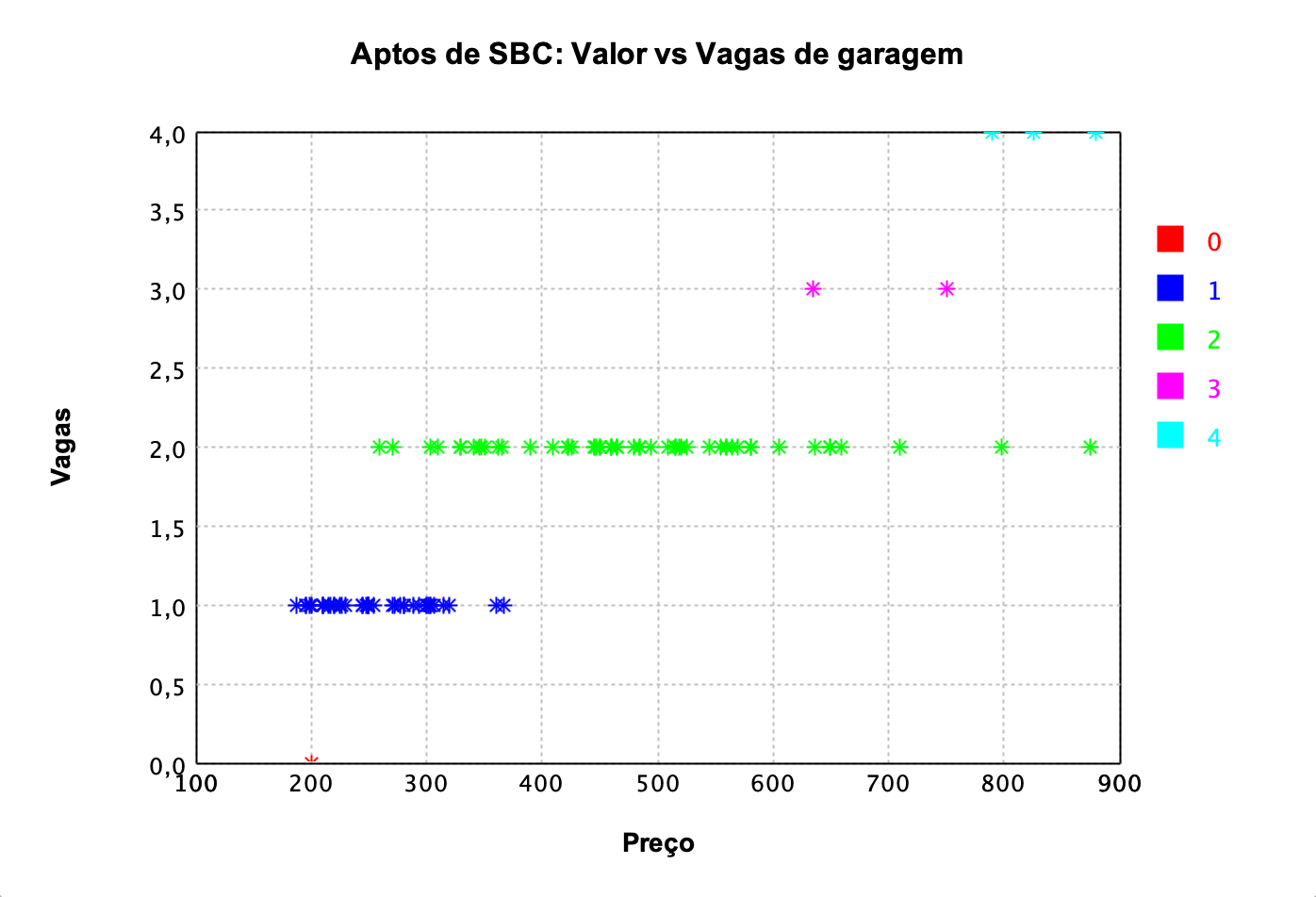
Também podemos visualizar se três variáveis podem ajudar a definir o preço do apartamento. Na Figura 4 temos o gráfico de dispersão usando as variáveis metros, valor e quantidade de quartos.
Figura 4: Gráfico de dispersão entre metros, valor e a quantidade de quartos do apartamento.
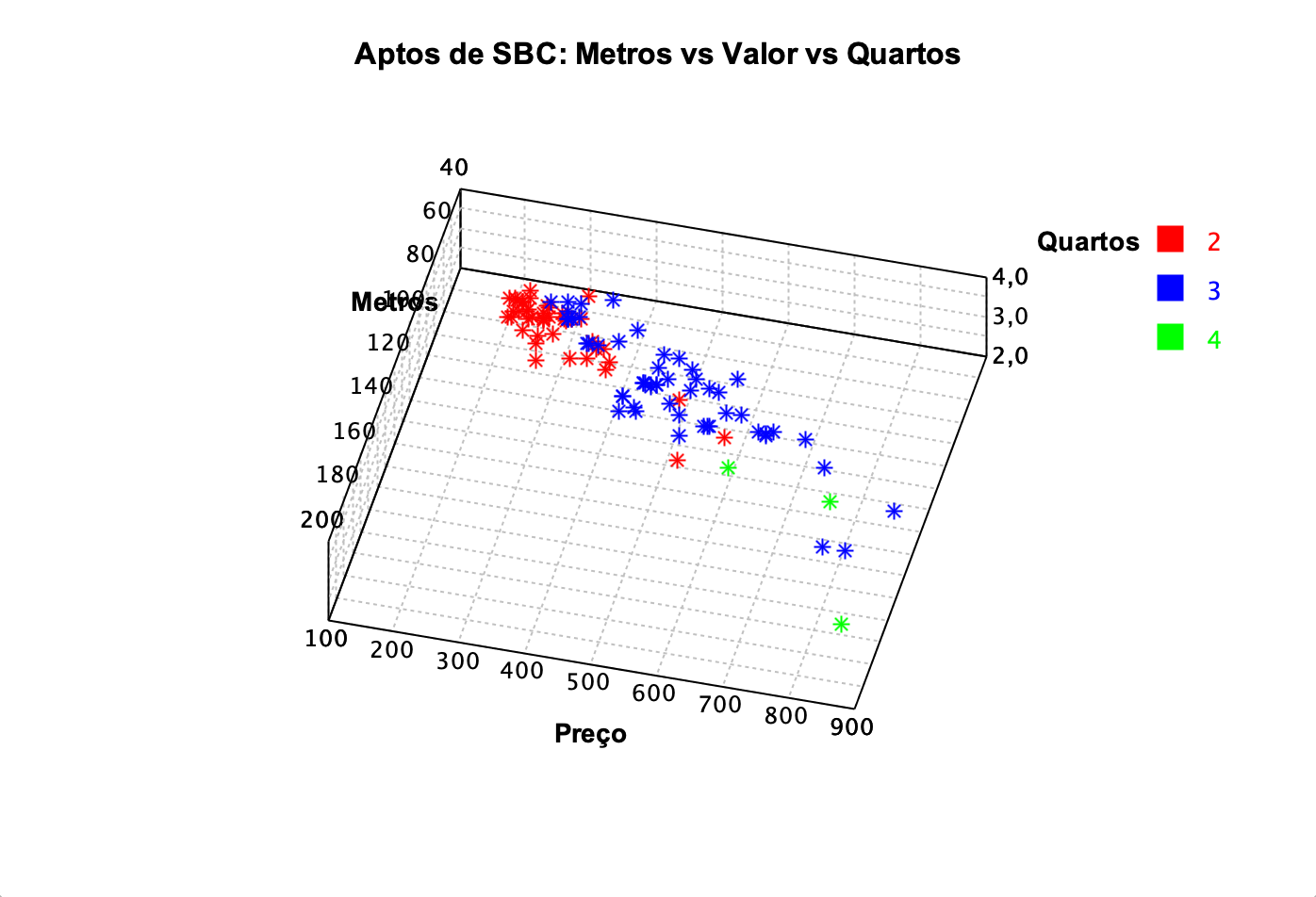
Na Figura 5 temos o gráfico de dispersão usando as variáveis metros, valor e quantidade de vagas de garagem.
Figura 5: Gráfico de dispersão entre metros, valor e a quantidade de vagas de garagem.
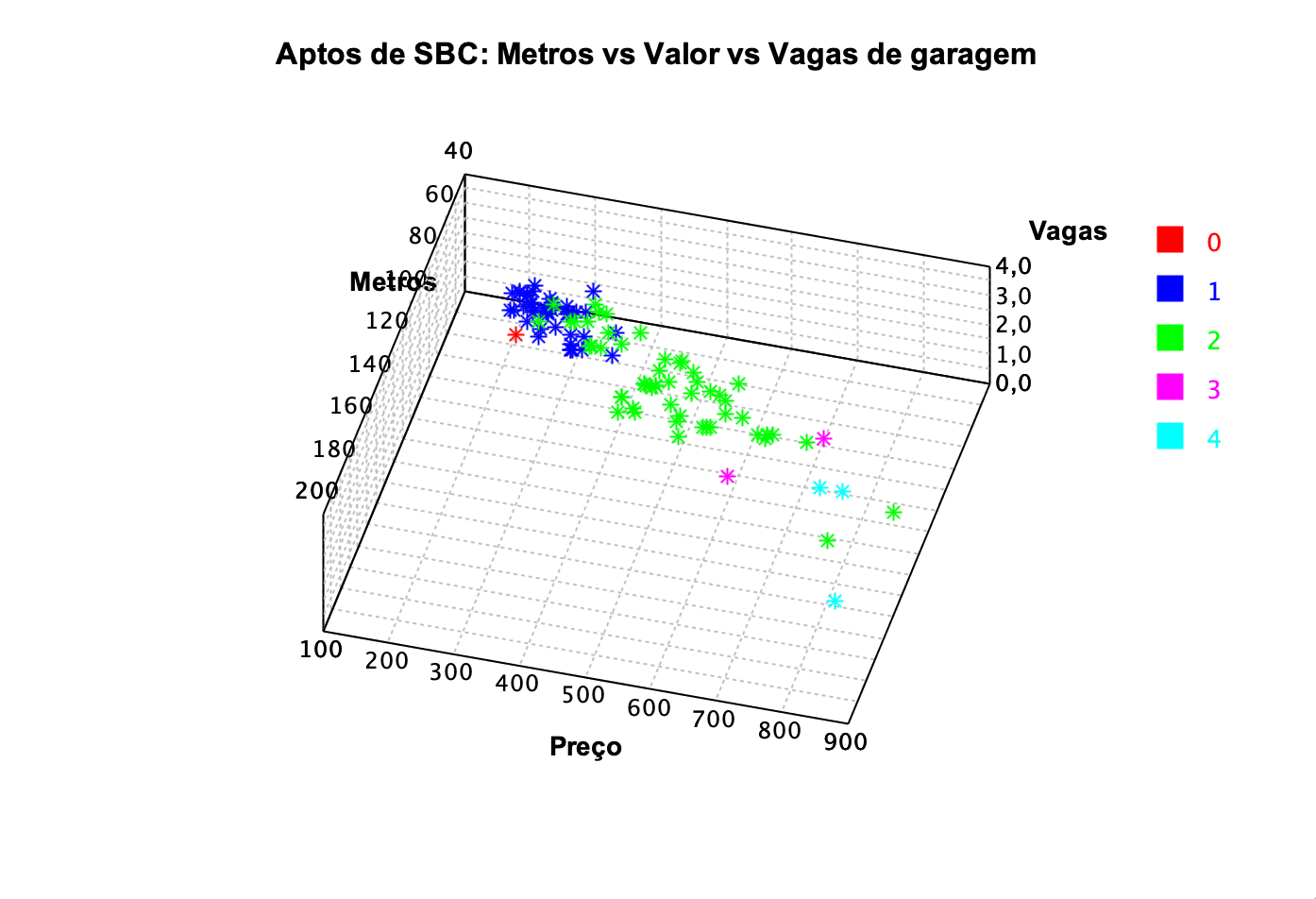
Poderíamos fazer esta mesma combinação para outras 3 variáveis, mas acredito que já deu para ver que algumas variáveis influenciam no valor do apartamento.
Agora usando Regressão Linear Múltipla, vamos responder a pergunta Qual o valor de um apartamento reformado de 100m² com 3 quartos e 2 vagas de garagem no bairro Rudge Ramos?
Qual o valor de um apartamento reformado de 100m² com 3 quartos e 2 vagas no bairro Rudge Ramos?
Vamos dar uma olhada nas primeiras linhas do arquivo csv.
| metros | valor | quartos | vagas | reformado | bairro |
|---|---|---|---|---|---|
| 43 | 300 | 2 | 1 | 1 | Assunção |
| 50 | 210 | 2 | 1 | 1 | Demarchi |
| 65 | 340 | 2 | 2 | 1 | Nova Petrópolis |
| 70 | 330 | 2 | 2 | 0 | Centro |
| 81 | 485 | 2 | 2 | 0 | Independência |
| 93 | 447 | 3 | 2 | 0 | Baeta Neves |
| 107 | 560 | 3 | 2 | 0 | Vila Lusitânia |
Para utilizarmos Regressão Linear Múltipla primeiro precisamos preparar este dataset, porque todos os dados que serão utilizados precisam estar no formato numérico.
O nome dos bairros está no formato categórico, neste conjunto de dados que coletei, estão inclusos apartamentos de 17 bairros diferentes de SBC:
| Assunção | Irajá | Planalto |
| Baeta Neves | Jardim do Mar | Rudge Ramos |
| Centro | Jordanopolis | Santa Teresinha |
| Demarchi | Nova Petrópolis | Taboão |
| Ferrazópolis | Pauliceia | Vila Lusitânia |
| Independência | Piraporinha |
Um dos métodos (existem vários) para obter uma representação numérica a partir dos nomes dos bairros é usando a binarização.
Binarização
A ideia da binarização é gerar um conjunto de características contendo o valor 0 ou 1, que servem para representar um valor categórico. Então dado os 17 bairros a seguir:
| 1- Assunção | 7- Irajá | 13- Planalto |
| 2- Baeta Neves | 8- Jardim do Mar | 14- Rudge Ramos |
| 3- Centro | 9- Jordanopolis | 15- Santa Teresinha |
| 4- Demarchi | 10- Nova Petrópolis | 16- Taboão |
| 5- Ferrazópolis | 11- Pauliceia | 17- Vila Lusitânia |
| 6- Independência | 12- Piraporinha |
Vamos obter 17 novas características, e para cada bairro teremos uma característica contendo o valor 1 e as demais contendo o valor 0 (zero). Exemplo:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | (bairro Rudge Ramos) |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | (bairro Ferrazópolis) |
Binarização com o Pandas
O pandas possui uma implementação para realizar a binarização por meio do método get_dummies, exemplo:
1
2
3
4
import pandas as pd
df = pd.read_csv('aptos.csv')
bairros = pd.get_dummies(df[['bairro']]).values
Neste código carregamos o dataset e geramos um novo dataset contendo apenas as características do bairro no formato binarizado, o resultado dos bairros das 3 primeiras linhas do dataset é:
1
2
3
bairros[0] = [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1]
bairros[1] = [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1]
bairros[2] = [0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0]
Agora que já sabemos como tratar a coluna bairro, podemos ajustar o dataset e prosseguir com o treino da Regressão Múltipla.
Regressão Linear Múltipla com scikit-learn
Para realizar o treinamento, vamos separar o dataset em duas parte: X será uma matriz para representar as características de entrada e y representa um vetor com os valores esperados pela regressão.
1
2
X = pd.get_dummies(df[['metros', 'quartos', 'vagas', 'reformado', 'bairro']]).values
y = df[['valor']].values
A seguir temos as primeiras linhas da matriz X:
1
2
3
[107 3 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1]
[107 3 2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1]
[49 2 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0]
A seguir temos as primeiras linhas do vetor y:
1
2
3
4
5
[[560]
[555]
[196]
...
[200]]
Agora vamos treinar a Regressão Linear Múltipla:
1
2
model = LinearRegression()
model.fit(X, y)
A variável model agora representa um modelo de Regressão Linear Múltipla que foi treinado para predizer o valor de um apartamento com base nas demais informações.
Para realizar a predição precisamos montar um vetor contendo todas as características, incluindo as que representam o bairro no formato binarizado, exemplo:
1
[100, 3, 2, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0]
Executando a predição:
1
print("Um apto de 100m com 3 quartos, 2 vagas, reformado no bairro Rudge Ramos custa: %.2f" % model.predict([[100, 3, 2, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0]]))
Temos o resultado:
1
Um apto de 100m com 3 quartos, 2 vagas, reformado no bairro Rudge Ramos custa: 491.18
Se quiser faça um teste ai, usando o dataset de aptos responda quanto custa um apartamento de 100m, com 3 quartos, 2 vagas no bairro Centro?
Continuando os estudos
Agora que você já sabe como usar a Regressão Linear Multipla, altere esse exemplo, crie ou use um dataset do seu interesse ou para resolver algum problema na empresa que você trabalha.