Regressão Linear Simples

A Regressão Linear Simples é usada quando queremos entender a relação que existe entre duas variáveis quantitativas, como: o valor e a metragem de um apartamento, ou as horas de estudo e a nota da prova, investimento em marketing e lucro das vendas, etc.
Utilizando um conjunto de dados podemos identificar essa relação existente entre duas variáveis e isso pode ser usado para tentar predizer um valor.
Qual o valor do apto em SBC?
Imagina que você está querendo comprar ou vender um imóvel, então resolve pesquisar em alguns sites como estão os preços dos imóveis próximos da sua localidade. Procurando na Internet você encontrou alguns imóveis e anotou o tamanho de metros quadrados e o preço. Esses são alguns valores de apartamentos em SBC.
| m² | preço |
|---|---|
| 45 | R$227.000 |
| 51 | R$249.000 |
| 64 | R$340.000 |
| 71 | R$410.000 |
| 82 | R$495.000 |
| 91 | R$570.000 |
| 106 | R$636.000 |
Digamos que você não encontrou um apartamento com a metragem que você queria ou encontrou vários com a mesma metragem, mas valores diferentes. Como podemos fazer para encontrar o valor de um apartamento de 100 m²?
Visualizando os dados
Vamos começar olhando as amostras que coletamos. Anotei os dados de 100 apartamentos de SBC e coloquei nesse csv, mas sugiro você fazer o dataset com valores de apartamentos próximos de onde você mora.
Na Figura 1 temos um gráfico de dispersão mostrando como estão dispostos os dados de m² e valor dos apartamentos.
Figura 1: Dispersão dos valores de m² e valor dos apartamentos.
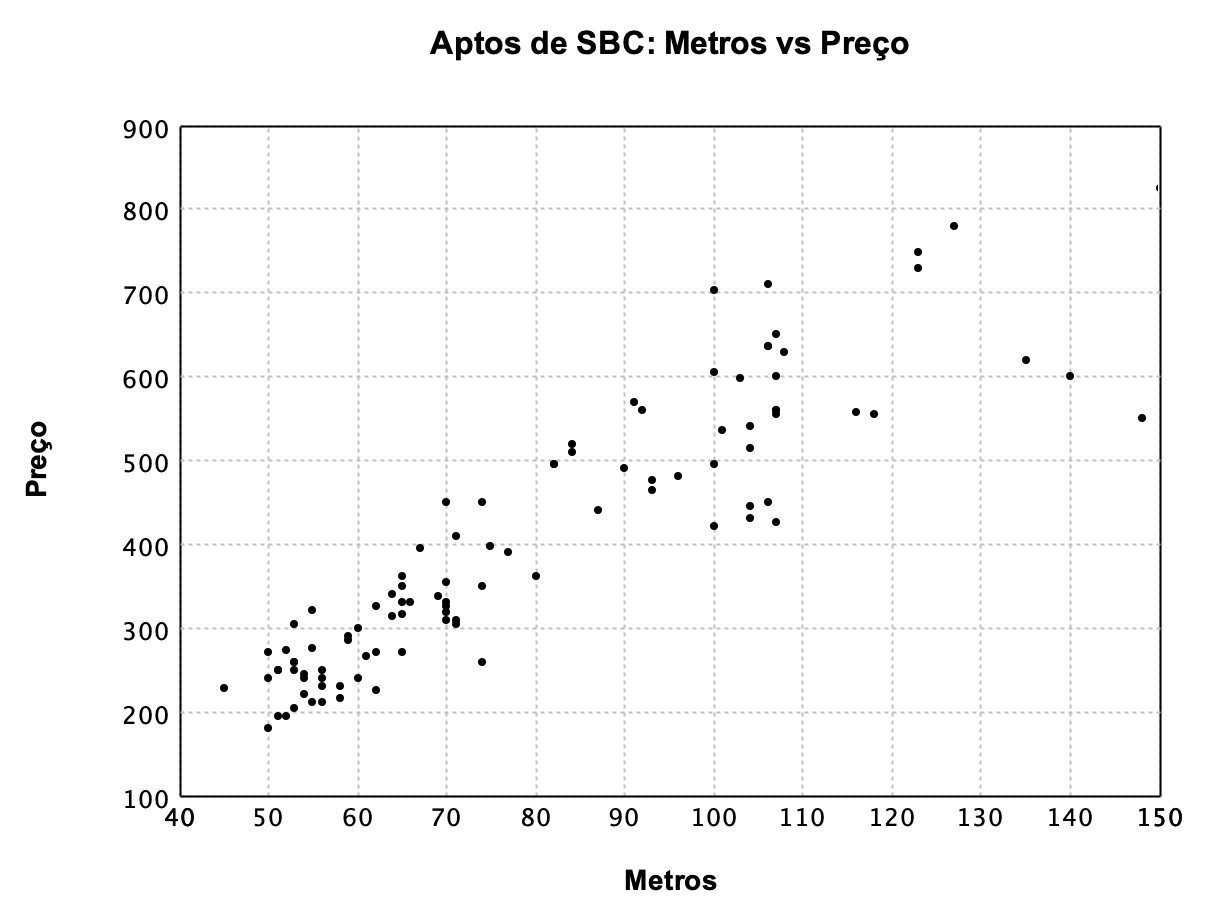
No gráfico, podemos reparar uma correlação nessas duas variáveis, porque quanto mais m² tem o apartamento, mais caro esse apartamento custa.
ScatterPlot no Java
Para gerar o gráfico vou usar a biblioteca Smile e vou mostrar o gráfico dentro de um JFrame.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import java.awt.Color;
import javax.swing.JFrame;
import org.apache.commons.csv.CSVFormat;
import smile.data.DataFrame;
import smile.io.CSV;
import smile.plot.swing.ScatterPlot;
public class GraficoDispersao {
public static void main(String[] args) throws Exception {
CSVFormat format = CSVFormat.DEFAULT.withFirstRecordAsHeader();
DataFrame df = new CSV(format).read("./aptos-metro-valor.csv");
JFrame frame = new JFrame();
frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
frame.setSize(700, 500);
frame.add(ScatterPlot.of(df, "metros", "valor", '@', Color.BLACK)
.canvas()
.setTitle("Aptos de SBC: Metros vs Preço")
.setAxisLabels("Metros", "Preço")
.panel());
frame.setVisible(true);
}
}
ScatterPlot no Python
Para facilitar a montagem deste gráfico de dispersão, podemos usar a biblioteca Pandas para carregar os dados e também a matplotlib para gerar o gráfico:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
from matplotlib import pyplot as plt
import pandas as pd
df = pd.read_csv('aptos-metro-valor.csv')
metros = df['metros'].values
preco = df['valor'].values
plt.scatter(metros, preco, color='black')
plt.xlim(0, 160)
plt.ylim(0, 1000)
plt.title("Aptos de SBC: Metros vs Preco")
plt.xlabel("Metros")
plt.ylabel("Preco")
plt.show()
Qual o valor de um apartamento de 100m² em SBC?
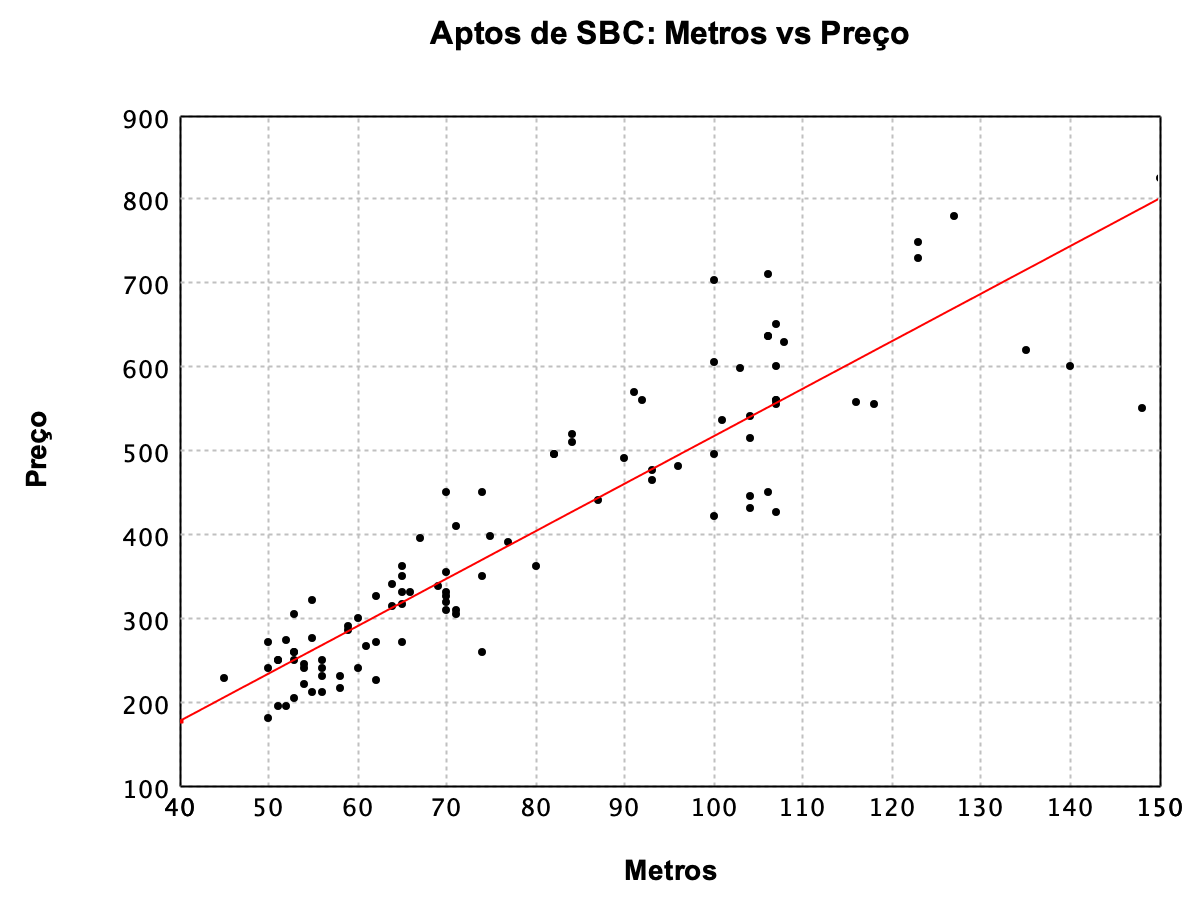
Mas quanto custa um apartamento de 100m² em SBC? Se desenharmos uma reta que representa o crescimento do valor conforme aumenta o m², como na Figura 2.
Figura 2: Gráfico do crescimento do valor conforme aumenta o m².
Se desenharmos uma linha tracejada vertical no valor dos 100m² até a linha de crescimento, é outra linha tracejada na horizontal como na Figura 3. Podemos chutar que um apartamento de 100m² custa uns R$510.000.
Figura 3: Tentando predizer o valor de um apartamento de 100m².
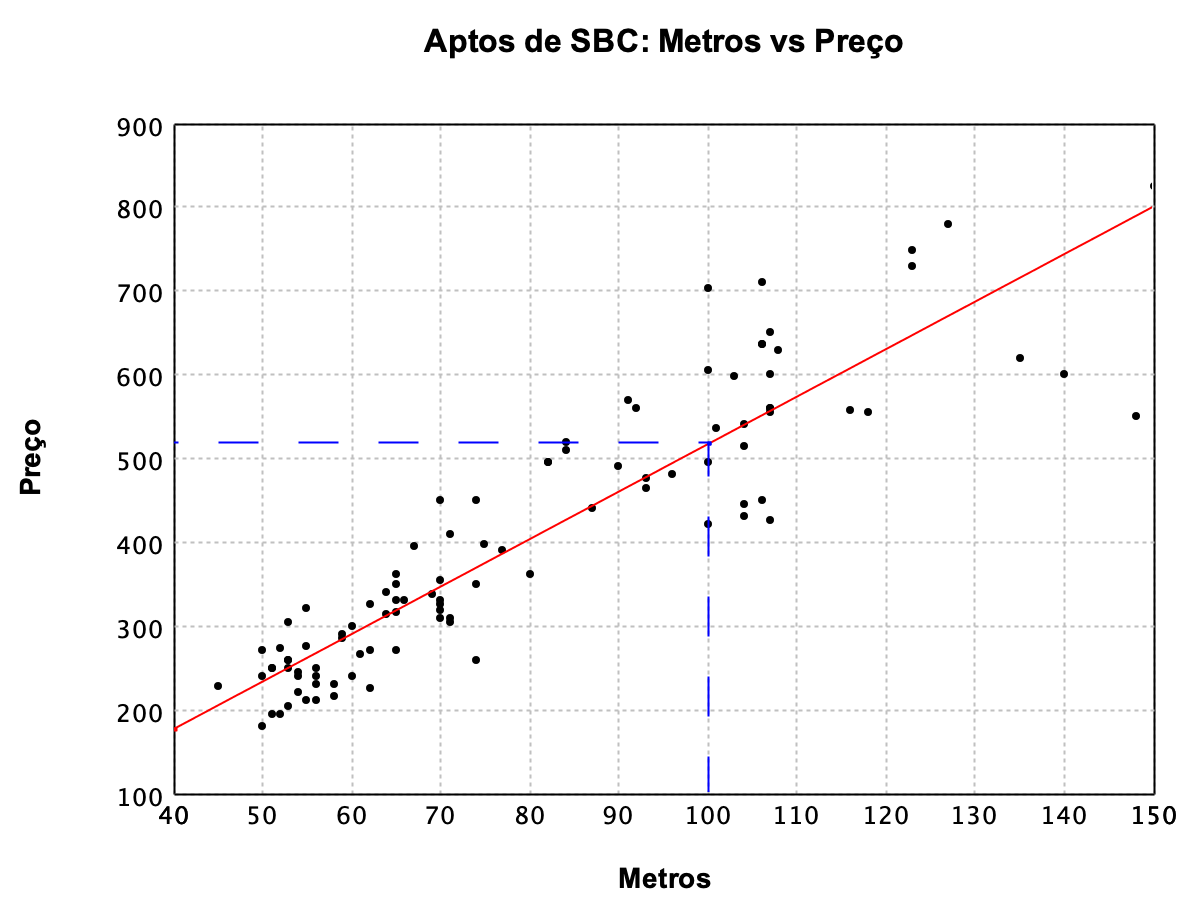
Mas o que fizemos foi tentar traçar uma reta que representa a correlação dos dados, mas como fazemos para encontrar os valores dessa reta ou ter certeza que essa é a melhor reta?
Regressão Linear
Regressão linear é quando podemos utilizar uma função de 1º grau (igual as que aprendemos no 1° ano do ensino médio) que melhor representa a correlação linear entre as variáveis.
Como: f(x) = α + β.x
Aplicando no exemplo apartamentos, esperamos que ao informar o valor de x que pode representar o m², a função retorna o valor do preço.
Função de predição
A função usada para predizer a reta é:
f(x) = α + β.x
Implementação no Java:
1
2
3
public double predicao(double alpha, double beta, double x) {
return alpha + beta * x;
}
Implementação no Python:
1
2
def predicao(alpha, beta, x):
return alpha + beta * x
Mas qual o valor das variáveis α e β?
Sabemos qual função usar e como escrever o código dessa função, também temos o valor de x, que neste exemplo representa os m² do apartamento, mas qual o valor vamos passar para as variáveis alpha e beta?
Se achamos que um apartamento de 100m² custa R$510.000, podemos chutar que alpha = 500.000 e beta = 100. Porque:
1
2
f(100) = 500.000 + 100 * 100
f(100) = 510.000
Parece bom o nosso chute, mas e se tentarmos predizer o valor de um apartamento de 60m²?
1
2
f(60) = 500.000 + 100 × 60
f(60) = 506.000
O valor de uma apartamento de 60m² é muito similar ao de 100m² e bem longe da realidade desses dados. Então não dá para simplesmente ficar chutando valores de alpha e beta.
Como podemos encontrar os valores de alpha e beta?
Quando desenhamos uma reta que auxilia na predição de um novo valor com base nos dados já existentes, o que estamos querendo fazer é identificar com base em cada um dos pontos do dataset qual a menor distância entre esse ponto e a reta, porque quanto menor for essa distância menor será o erro de predição.
Solução dos mínimos quadrados
A ideia da solução dos mínimos quadrados é reduzir o quadrado do erro médio total, e isso é feito obtendo a menor diferença entre uma amostra e o valor predito.
Essa implementação foi feita com base no exemplo apresentado no cápitulo 14 do livro Data Science do Zero.
Observação: se você quiser entender um pouco melhor como funciona a solução dos mínimos quadrados, como é feita a derivada para gerar as funções para calcular alpha e beta, recomendo esse vídeo que mostra bem passo a passo.
Implementação no Java:
Vou usar as funções de correlação, desvio médio e média da classe smile.math.MathEx a biblioteca Smile.
1
2
3
4
5
public static double[] minimos_quadrados(double[] x, double[] y) {
double beta = cor(x, y) * sd(y) / sd(x);
double alpha = mean(y) - beta * mean(x);
return new double[] {alpha, beta};
}
Implementação no Python
Vou usar as funções de correlação, desvio médio e média do NumPy.
1
2
3
4
def minimos_quadrados(x, y):
beta = np.corrcoef(x, y)[0, 1] * np.std(y) / np.std(x)
alpha = np.mean(y) - beta * np.mean(x)
return alpha, beta
Treinando e predizendo valores com a Regressão Linear
Agora vamos carregar o dataset com os 100 apartamentos, calcular o valor de alpha e beta e por fim predizer o valor de um apartamento de 100m².
Juntando o código Java:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import org.apache.commons.csv.CSVFormat;
import smile.data.DataFrame;
import smile.io.CSV;
import static smile.math.MathEx.*;
public class RegressaoLinear {
public static void main(String[] args) throws Exception {
CSVFormat format = CSVFormat.DEFAULT.withFirstRecordAsHeader();
DataFrame df = new CSV(format).read("./aptos-metro-valor.csv");
double[] x = df.intVector("metros").toDoubleArray();
double[] y = df.intVector("valor").toDoubleArray();
System.out.printf("Um apto de 100m custa: %.2f", regressaoLinear(x, y, 100));
}
public static double predicao(double alpha, double beta, double x) {
return alpha + beta * x;
}
public static double[] minimos_quadrados(double[] x, double[] y) {
double beta = cor(x, y) * sd(y) / sd(x);
double alpha = mean(y) - beta * mean(x);
return new double[] {alpha, beta};
}
public static double regressaoLinear(double[] x, double[] y, double z) {
double[] alpha_beta = minimos_quadrados(x, y);
System.out.println("alpha: " + alpha_beta[0]); // -48.1212291326
System.out.println("beta: " + alpha_beta[1]); // 5.6647974510
return predicao(alpha_beta[0], alpha_beta[1], z);
}
}
Juntando o código Python:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import numpy as np
import pandas as pd
def predicao(alpha, beta, x):
return alpha + beta * x
def minimos_quadrados(x, y):
beta = np.corrcoef(x, y)[0, 1] * np.std(y) / np.std(x)
alpha = np.mean(y) - beta * np.mean(x)
return alpha, beta
df = pd.read_csv('aptos-metro-valor.csv')
x = df[['metros']].values.T[0]
y = df[['valor']].values.T[0]
alpha, beta = minimos_quadrados(x, y)
print(alpha) # -56.7434863885
print(beta) # 5.72587800683
valor = predicao(alpha, beta, 100)
print("Um apto de 100m custa: %.2f" % valor)
Saída:
1
Um apto de 100m custa: 515.84
Então um apartamento de 100m² custa R$515,84, se calcularmos o preço de um apto de 60m² temos o valor de R$286,81.
Agora que sabemos implementar a Regressão Linear na mão, não precisamos ficar implementado em cada projeto que formos desenvolver, podemos usar uma biblioteca que já tem essa implementação.
Regressão Linear com Smile
No Smile temos uma implementação da Regressão Linear na classe OLS:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import org.apache.commons.csv.CSVFormat;
import smile.data.DataFrame;
import smile.data.formula.Formula;
import smile.io.CSV;
import smile.regression.LinearModel;
import smile.regression.OLS;
public class RegressaoLinearSmile {
public static void main(String[] args) throws Exception {
CSVFormat format = CSVFormat.DEFAULT.withFirstRecordAsHeader();
DataFrame df = new CSV(format).read("./aptos-metro-valor.csv");
LinearModel linear = OLS.fit(Formula.lhs("valor"), df);
double valor = linear.predict(new double[] {100});
System.out.printf("Um apto de 100m custa: %.2f", valor);
}
}
Regressão Linear com scikit-learn
No Scikit-learn temos uma implementação pronta da Regressão Linear:
1
2
3
4
5
6
7
8
9
10
11
from sklearn.linear_model import LinearRegression
import pandas as pd
df = pd.read_csv('aptos-metro-valor.csv')
x = df[['metros']].values
y = df[['valor']].values
model = LinearRegression()
model.fit(x, y)
print("Um apto de 100m custa: %.2f" % model.predict(100))
Continuando os estudos
Agora que você já sabe como usar a Regressão Linear, altere esse exemplo, ao invés de predizer o valor, tente inverter e predizer os metros quadrados a partir do valor do apartamento. Uma outra sugestão é usar outro dataset, monta o seu dataset com algo que você tenha interesse ou algo que pode ser aplicado no seu trabalho.
Mas será que calcular o valor do apartamento pelo tamanho do m² é a melhor forma de obter o valor? Acho que tem outras variáveis que podem ajudar a obter um valor mais coerente com a realidade, e se usar também o bairro, quantidade de vagas na garagem, se o apartamento é novo ou já está reformado, etc, será que teríamos um valor melhor? Vou comentar sobre isso no próximo post sobre Regressão Linear Múltipla.