Revisão de álgebra linear em Python
Numpy
A biblioteca de computação científica NumPy facilita muito a manipulação algébrica de matrizes de n dimensões.
Para importar a biblioteca numpy:
1
import numpy as np
No site do NumPy também tem um tutorial de como começar a usar.
O tipo básico de dados é o ndarray que representa um array multidimensional.
1
2
notas = np.array([7.8, 9.1, 8.6, 7.4])
aptos = np.array([104, 515, 1], [140, 635, 1], [50, 210, 0])
Álgebra Linear
Vetores
Vetores podem ser entendidos como pontos no espaço e podemos representar os dados usando vetores. Exemplo: os dados que representam um apartamento, as notas de um aluno, os valores que compõem o preço de um produto, entre outros, podem ser armazenados em um vetor.
No Python representamos um vetor como um array do NumPy, então se temos apenas a informação da quantidade de m², temos um vetor com um eixo:
1
apto = np.array([67])
Adicionando a informação do valor do apartamento no vetor, teremos um vetor com dois eixos:
1
apto = np.array([67, 250])
Se continuarmos incluindo mais uma informação como a quantidade de quartos, teremos um vetor três eixos:
1
apto = np.array([67, 250, 2])
E podemos continuar adicionando informações no vetor e a cada novo valor aumentamos um eixo do vetor.
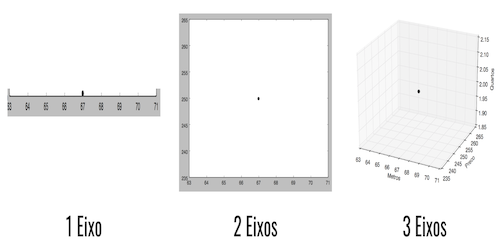
A Figura 1 mostra como um vetor pode ser representado visualmente até o terceiro eixo.
Figura 1: Visualizando um vetor de 1, 2 e 3 dimensões.
Métodos úteis da np.array
1
2
3
4
x = np.array([1, 2, 3, 4])
x.sum() # soma dos valores do vetor = 10
x.min() # menor valor do vetor = 1
x.max() # maior valor do vetor = 4
Soma de vetores
Dois ou mais vetores (de tamanho igual) podem ser somados e para isso é calculado a soma de cada elemento nas mesmas posições do vetor, exemplo:
Exemplo: quando temos um vetor com valores de almoço e outro vetor com valores de gorjetas, podemos somar os dois vetores para obter o valor total de cada refeição.
1
2
3
x = np.array([1, 2, 3, 4])
y = np.array([5, 6, 7, 8])
soma = x + y #[6, 8, 10, 12]
Soma escalar
Também é possível fazer a soma escalar (com um número) no vetor, então um valor é somado a cada elemento do vetor. Exemplo, suponha um conjunto de média de notas dos alunos, e o professor bonzinho resolve dar 0.5 pontos para cada aluno:
1
2
notas = np.array([6.5, 8.0, 7.5, 4.5, 9.0, 6.5, 6.0, 5.5, 7.0, 8.0, 6.5, 7.5])
soma = notas + 0.5 #[7.0, 8.5, 8.0, 5.0, 9.5, 7.0, 6.5, 6.0, 7.5, 8.5, 7.0, 8.0]
Operações do array no Numpy
Com o novo vetor de notas, queremos saber quais os alunos obtiveram nota maior ou igual a 7.0 e foram aprovados. Para isso, podemos aplicar uma comparação a cada elemento do vetor, exemplo:
1
2
3
4
aprovados = soma >= 7.0
# o resultado é um vetor de booleanos:
# array([True, True, True, False, True, True, False, False, True, True, True, True], dtype=bool)
# que indica com True as notas que são maior ou igual a 7,0 e False as notas menores que 7,0.
E contar quantos valores são True, portanto tem nota maior ou igual a 7,0:
1
qtdAprovados = sum(soma >= 7.0) #9
O mesmo pode ser feito para saber quantos alunos tiveram a nota menor que 7,0 e foram reprovados. Podemos aplicar uma comparação a cada elemento do vetor, exemplo:
1
2
reprovados = soma < 7.0
# array([False, False, False, True, False, False, True, True, False, False, False, False], dtype=bool)
E contar quantos valores são True, portanto tem nota menor que 7,0:
1
qtdReprovados = sum(soma < 7.0) # 3
Multiplicação de vetores
Dois ou mais vetores podem ser multiplicados e para isso é calculado a multiplicação de cada elemento nas mesmas posições do vetor, exemplo:
1
2
3
x = np.array([1, 2, 3, 4])
y = np.array([5, 6, 7, 8])
mult = x * y #[5, 12, 21, 32]
Se temos um vetor com as notas de um aluno:
1
notas = np.array([8.0, 7.0, 7.5, 9.5, 10.0])
E temos um vetor com o peso que representa cada uma das notas na disciplina:
1
pesos = np.array([0.2, 0.1, 0.1, 0.3, 0.3])
Se multiplicarmos os dois vetores e somar seus valores, temos como resultado a nota que este aluno teve na disciplina:
1
notaFinal = sum(notas * pesos)
Multiplicação de escalar
Também é possível fazer a multiplicação escalar (com um número) no vetor, então um valor é multiplicado a cada elemento do vetor. Exemplo, suponha que temos um vetor os valores pagos com comida em um restaurante:
1
valores = np.array([18.0, 16.5, 17.0, 19.5, 18.5])
E queremos calcular 10% de gorjeta para cada um dos valores:
1
gorjeta = valores * 0.1 #[1.8, 1.65, 1.7, 1.95, 1.85]
Se quiser saber o total de gorjeta é só somar o vetor sum(gorjeta).
Produto escalar de vetores
A Figura 2 mostra o produto escalar de dois vetores.
Figura 2: Equação do produto escalar de dois vetores.
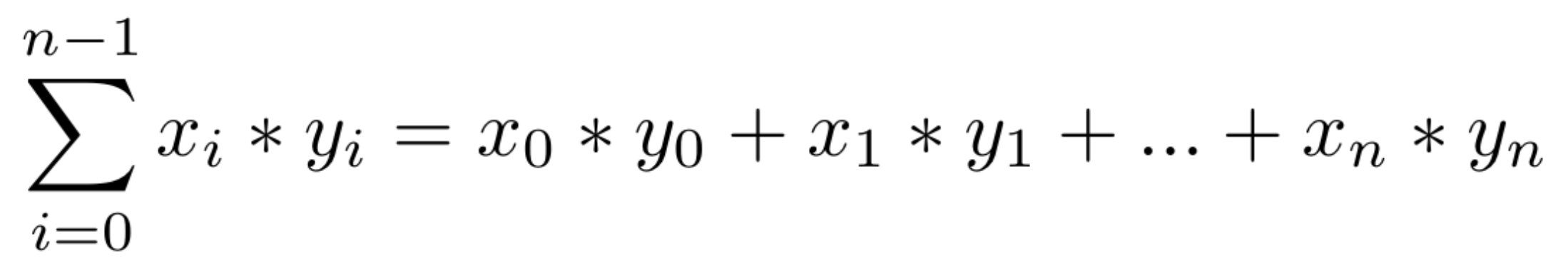
sendo x e y, dois vetores de tamanho iguais e n o tamanho dos vetores, o produto escalar é a somatória da multiplicação de dois vetores, exemplo:
1
2
3
x = np.array([1, 2, 3, 4])
y = np.array([5, 6, 7, 8])
prod = np.dot(x, y) # 70
Para calcular a soma dos quadrados de um vetor, também podemos usar o produto escalar como mostrado na Figura 3.
Figura 3: Soma dos quadrados de um vetor.
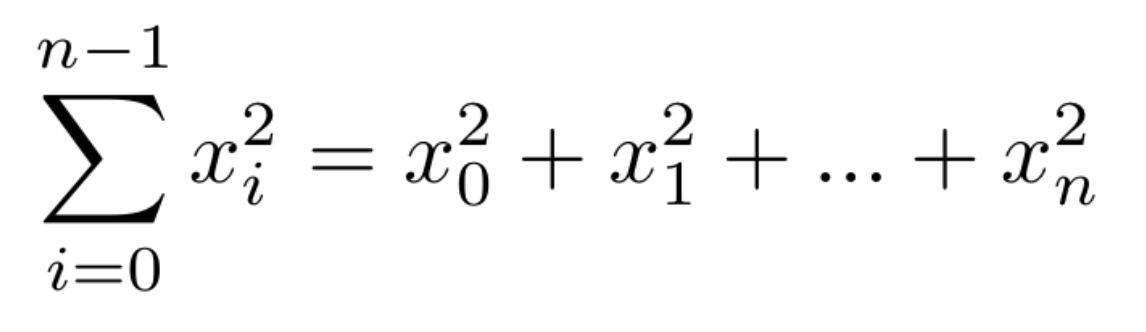
1
2
x = np.array([1, 2, 3, 4])
prod = np.dot(x, x) # 30
Porque obtemos como resultado a soma da multiplicação do vetor x por ele mesmo.
Distância entre vetores
Na Figura 4 temos o vetor [1,4] (quadrado verde) e um vetor [2,1] (quadrado azul). Temos um novo vetor [4,2] (triângulo vermelho), mas gostaríamos de classificar este novo vetor como quadrado verde ou azul. Para isso podemos verificar qual o quadrado mais próximo e usar a mesma cor, mas qual quadrado está mais perto do triângulo?
Figura 4: Distância entre vetores.
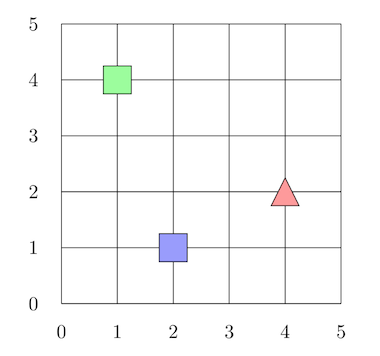
Na Figura 5 podemos perceber que o quadrado azul está mais próximo do triângulo vermelho, então podemos classificar este novo vetor como um quadrado azul.
Figura 5: Distância entre vetores.
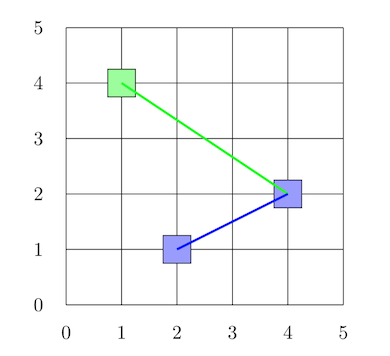
Uma das formas de calcular a distância entre vetores é usando a Distância Euclidiana, que é dada pela equação da Figura 6.
Figura 6: Distância Euclidiana.
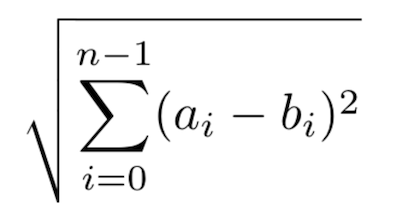
Então, na Figura 7 calculamos o distância euclidiana entre o vetor [1,4] (quadrado verde) com o vetor [4,2] (triângulo vermelho).
Figura 7: Distância Euclidiana.
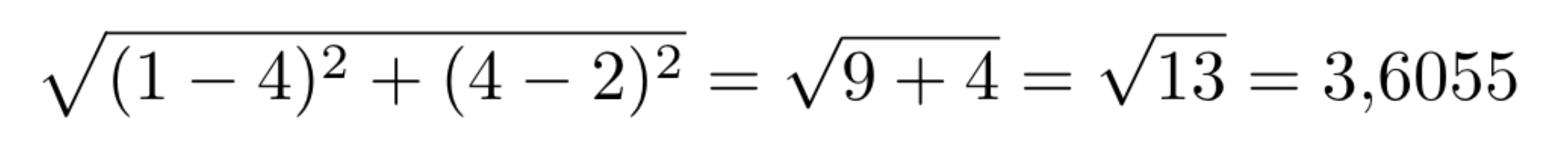
E na Figura 8 calculamos distância euclidiana entre o vetor [2,1] (quadrado azul) com o vetor [4,2] (triângulo vermelho).
Figura 8: Distância Euclidiana.
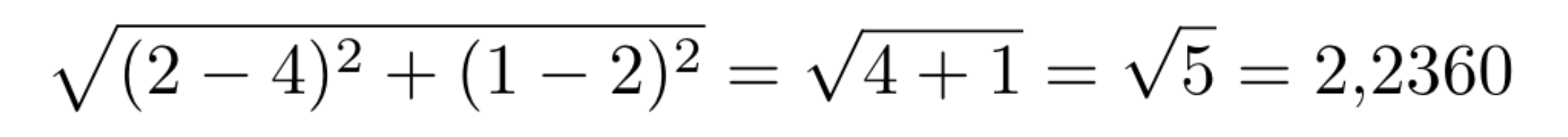
Portanto, sabemos que a menor distância é em relação ao quadrado azul.
Usando o Python, podemos calcular a distância entre os vetores:
1
2
3
qv = np.array([1,4]) # Quadrado verde
qa = np.array([2,1]) # Quadrado azul
tv = np.array([4,2]) # Triângulo vermelho
com:
1
2
distanciaQuadradoVerde = np.sqrt(sum((qv - tv) ** 2)) #3.6055
distanciaQuadradoAzul = np.sqrt(sum((qa - tv) ** 2)) #2.2360
Obs: O ** é utilizado para calcular o número da esquerda elevado ao número da direita. Exemplo 5² é calculado como 5 ** 2.
Matrizes
Matriz é formada por um conjunto de vetores, normalmente representada em maiúsculo, como A[m, n] que tem m linhas por n colunas. O Numpy tem o objeto matrix que representa uma matriz, exemplo:
1
2
A = np.matrix([[1, 2, 3, 4],
[5, 6, 7, 8]])
Nesse caso dizemos que a matriz A tem tamanho [2, 4], ou duas linhas e quatro colunas. Para acessar uma determinada posição da matriz precisamos informar os valores da linha e coluna, lembrando que os índices começam com zero, o valor da posição A[1, 3] é 8.
Soma de matrizes
A soma de matrizes:
1
2
3
4
5
6
7
8
A = np.matrix([[1, 2, 3, 4],
[5, 6, 7, 8]])
B = np.matrix([[1, 2, 3, 4],
[5, 6, 7, 8]])
SOMA = A + B
# [[ 2, 4, 6, 8],
# [10, 12, 14, 16]]
Transposta
Com o Numpy podemos obter facilmente a transposta de uma matriz:
1
2
3
4
5
6
A = np.matrix([[1, 2, 3, 4],
[5, 6, 7, 8]])
A.T # [[1, 5],
# [2, 6],
# [3, 7],
# [4, 8]]
Multiplicação de matrizes
Para multiplicar duas matrizes é necessário que uma matriz A tenha dimensão m x n enquanto que a matriz B tenha a dimensão n x m, como resultado temos uma matriz de dimensão m x m.
1
2
3
4
5
6
7
8
A = np.matrix([[1, 2, 3, 4],
[5, 6, 7, 8]])
B = np.matrix([[1, 2],
[3, 4],
[5, 6],
[7, 8]])
mult = A * B # [[ 50, 60],
# [114, 140]]