Estatística

Nesse post faço uma revisão sobre Álgebra Linear e como usar a biblioteca NumPy para realizar as operações, recomendo a leitura caso você nunca tenha usado o NumPy.

Média

A média é usada para obter facilmente um valor que representa a tendência central dos dados. Para calcular a média, soma-se os valores e divide pela quantidade de valores.

No Python podemos calcular a média como:

1
2
x = np.array([10500, 9200, 11000, 8900, 10100, 9800, 9600])
media = np.mean(x)  # média das vendas R$9.871,42

Mas a média é sensível a valores atípicos, muito fora do padrão, como a venda feita para um grande cliente no valor de R$100.000,00:

1
2
x = np.array([10500, 9200, 11000, 8900, 10100, 9800, 9600, 100000])
media = np.mean(x)

Que sobe a média de vendas para R$21.137,50, um valor longe dos demais valores de vendas.

Mediana

Quando a média não fornece mais um valor próximo da maioria dos valores, podemos utilizar a mediana que representa um valor que divide a distribuição de valores bem no meio.

Para calcular a mediana primeiro precisamos ordenar os valores:

1
2
3
x = np.array([10500, 9200, 11000, 8900, 10100, 9800, 9600, 100000])
x = np.sort(x)  # coloca os valores do vetor em ordem crescente.
# [8900, 9200, 9600, 9800, 10100, 10500, 11000, 100000]

Se a quantidade de valores for ímpar, a mediana é o valor que está bem no meio do conjunto de valores:

1
2
3
x = np.array([8900, 9200, 9600, 9800, 9900, 10100, 10500, 11000, 100000])
if (x.size % 2 == 1):  # quantidade de números é ímpar
    mediana = x[x.size / 2]

Portanto a mediana é 9900.

Mas se a quantidade de valores for par, a mediana é igual ao valor da soma das duas posições centrais dividido por dois:

1
2
3
x = np.array([8900, 9200, 9600, 9800, 10100, 10500, 11000, 100000])
else: # quantidade de números é par
    mediana = (x[x.size / 2 - 1] + x[x.size / 2]) / 2

Então a mediana é 9950. Mesmo com alguns números muito acima da média, o valor da mediana ainda devolve um valor central.

O código do cálculo da mediana é:

1
2
3
4
5
6
7
8
def mediana(x):
    n = len(x)
    x.sort() # os elementos de x precisam estar ordenados
    posicaoCentral = int(n / 2)
    if n % 2 == 1:
        return x[posicaoCentral]
    else:
        return (x[posicaoCentral - 1] + x[posicaoCentral]) / 2

Dispersão

A dispersão é uma medida que informa como os dados estão espalhados ou dispersos entre si. Para calcular a dispersão subtraímos o maior valor pelo menor valor, exemplo:

1
2
alturas = np.array([155, 158, 160, 162, 168, 170, 172, 175, 179, 180])
dispersao = max(alturas) - min(alturas)    #180 - 155 = 25

Quanto mais próximo do zero, menor é a dispersão dos dados.

Mas se temos um conjunto de dados que a maioria dos valores são iguais, mas com um ou outro maior e menor que a maioria, como:

1
alturas = np.array([155, 170, 170, 170, 170, 170, 170, 170, 170, 180])

Temos também uma dispersão alta dos dados:

1
dispersao = max(alturas) - min(alturas)    #25

Variância

A variância mostra como está a dispersão dos dados em relação a média.

1
2
3
4
5
6
alturas = np.array([155, 158, 160, 162, 168, 170, 172, 175, 179, 180])
# média = 167.90
np.var(alturas)    # 70.28
alturas = np.array([155, 153, 154, 152, 154, 150, 152, 155, 155, 150])
# média = 153.0
np.var(alturas)    # 3.39

Quanto menor a variância mais próximo os valores estão em relação a média.

Desvio padrão

O desvio padrão é calculado como a raiz quadrada da variância e também mostra como os dados se dispersão em relação a média.

1
2
3
alturas = np.array([155, 158, 160, 162, 168, 170, 172, 175, 179, 180])
# média = 167.90
np.std(alturas)    # 8.38

Portanto, podemos afirmar que a média das alturas é 1.67m com desvio para mais ou para menos de 8cm.

Covariância

A variância é utilizada quando queremos calcular a dispersão dos dados em relação a uma única variável, quando queremos calcular a dispersão com base em duas variáveis diferentes utilizamos a covariância. Dado uma matriz com altura e peso:

1
2
3
4
dados = np.matrix([[155, 158, 160, 162, 168, 170, 172, 175, 179, 180],
                   [49, 53, 53, 58, 68, 69, 75, 81, 84, 94]])
np.cov(dados)    #[[78.1, 131.82222222],
                   [131.82222222, 228.93333333]]

A covariância indica que quando a variável altura aumenta, a variável peso também aumenta.

Correlação

A correlação é utilizada para indicar como uma variável está relacionada com outra variável. Dado uma matriz de altura e pesos.

1
2
3
4
dados = np.matrix([[155, 158, 160, 162, 168, 170, 172, 175, 179, 180],
                   [49, 53, 53, 58, 68, 69, 75, 81, 84, 94]])
np.corrcoef(dados)  #[[ 1.0 ,  0.9858449],
                      [ 0.9858449,  1.0]]

Quanto mais próximo o valor for de 1, mais forte é a correlação entre as variáveis, se o valor for 0 então não há correlação e quanto mais próximo o valor for de -1, maior é a anticorrelação entre as variáveis.

Probabilidade

No curso de Sistema de Informação temos 54 alunos, sendo 9 mulheres e 45 homens. Escolhendo uma pessoa aleatoriamente, qual a probabilidade de escolher um homem ou uma mulher?

A Figura 1 mostra como calcular essa probabilidade.

Figura 1: Exemplo de probabilidade.

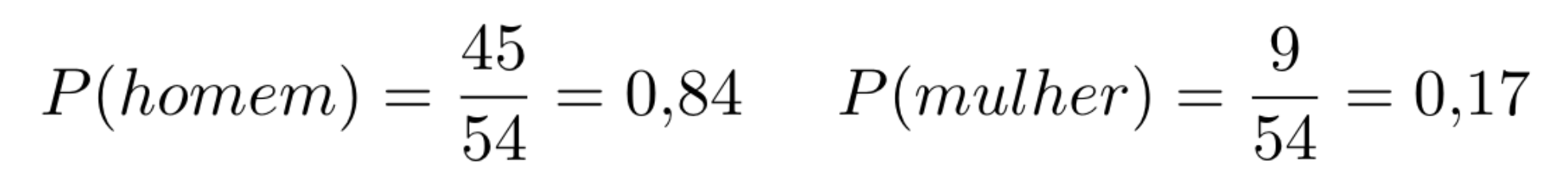
Portanto, a chance de escolher ao acaso um homem é de 84% e de escolher uma mulher e de 17%.

Variáveis aleatórias

Variáveis aleatórias são valores que possuem uma distribuição de probabilidade, exemplo: gerar um número aleatório entre 1 e 5. Como temos cinco valores possíveis: 1, 2, 3, 4 e 5, cada um destes valores tem 20% de chance de serem gerados aleatoriamente. No Python e no Numpy temos classes que geram valores aleatórios:

1
2
3
# gera cinco números entre [1 e 6), portanto valores 1, 2, 3, 4 e 5.
np.random.randint(1,6,5)
array([4, 2, 1, 4, 3])

Distribuições contínuas

Normalmente o valor gerado aleatoriamente está entre [0 e 1), exemplo:

1
2
np.random.rand(1)
array([ 0.28395951])

A função rand retorna x valores decimais entre [0 e 1). Neste caso todas os valores possíveis possuem a mesma probabilidade de serem gerados. Outro exemplo:

1
2
np.random.rand(5) # gera cinco números aleatórios entre [0 e 1).
array([ 0.61421351,  0.45312056,  0.64434587,  0.55447819,  0.26395382])

Distribuição normal

A distribuição normal (também chamada de gaussiana) é um valor aleatório gerado dentro de um intervalo de valores desejado, utiliza um valor de meio e um valor de desvio padrão, calculado pela equação da Figura 2.

Figura 2: Distribuição normal.

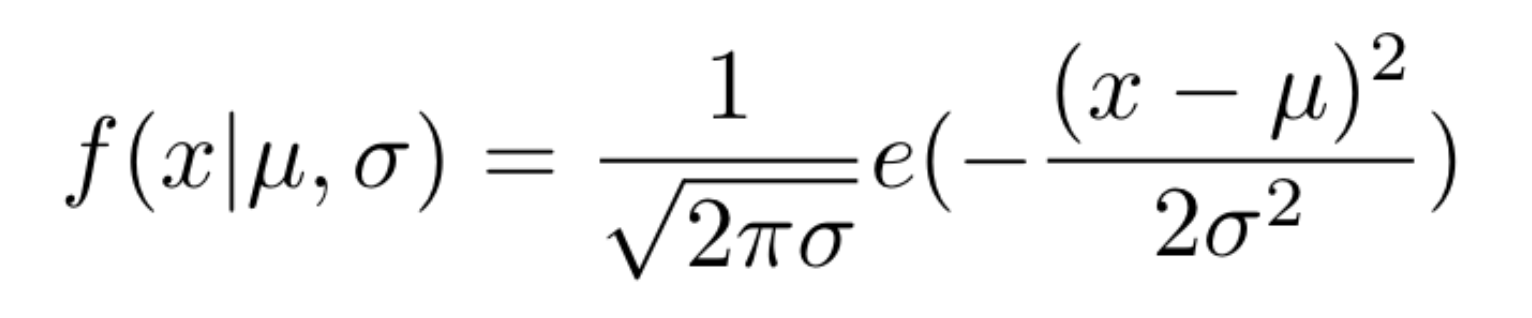
No qual μ (mu) representa o valor da média e σ (sigma) representa um desvio padrão (portanto para mais ou para menos).

Gerando uma distribuição normal, em que a média é o valor 0 e o desvio padrão é 1, temos um gráfico como mostrado na Figura 3.

Figura 3: Distribuição normal.

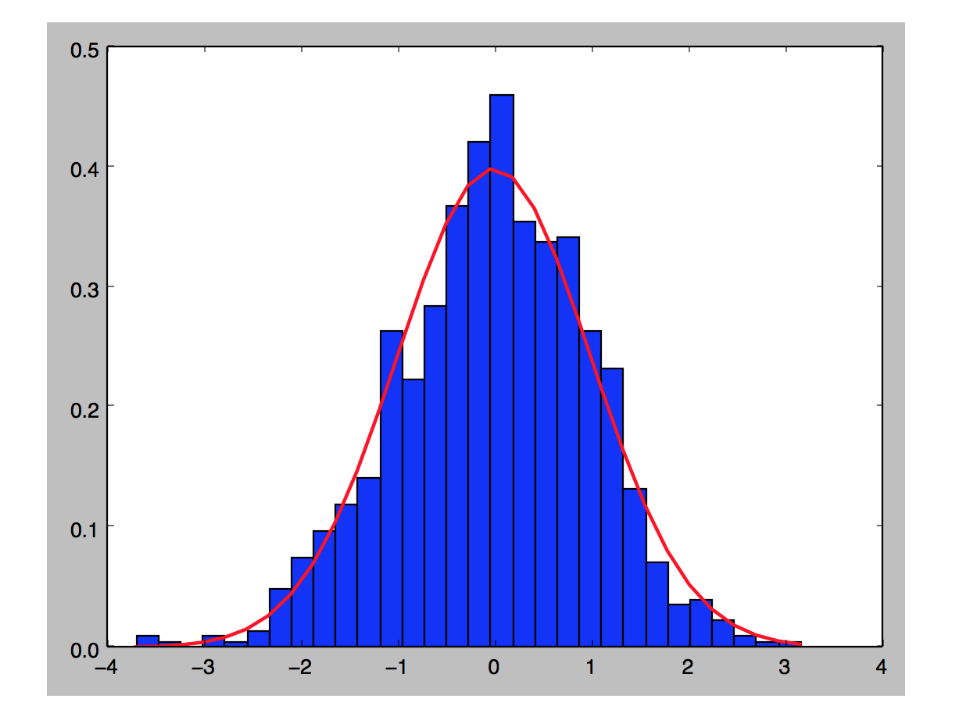
No qual podemos perceber que +ou- 70% dos valores gerados de modo aleatório serão entre -1 e 1.

O Numpy possui implementação para a distribuição normal:

1
2
3
4
5
np.random.normal(0,1)
1.0203127963258032

np.random.normal(0,1,5) # gera cinco números
array([-1.16986347, -1.55922361, -0.34402197,  0.91240606,  0.08705099])